题目内容
8.等比数列{an}的前n项和为Sn,已知S4=a2+a3+9a1,a5=32,则a1=( )| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | -2 |
分析 利用等比数列的通项公式即可得出.
解答 解:设等比数列{an}的公比为q,∵S4=a2+a3+9a1,a5=32,
∴a4=8a1即${a}_{1}{q}^{3}=8{a}_{1}$,${a}_{1}{q}^{4}$=32,
则a1=2=q.
故选:C.
点评 本题考查了等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
16.不等式|x+1|-|x-5|<4的解集为( )
| A. | (-∞,4) | B. | (-∞,-4) | C. | (4,+∞) | D. | (-4,+∞) |
3.运行如图所示的程序框图,则输出的数是7的倍数的概率为( )
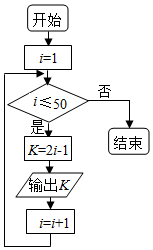

| A. | $\frac{4}{25}$ | B. | $\frac{8}{49}$ | C. | $\frac{7}{50}$ | D. | $\frac{14}{99}$ |
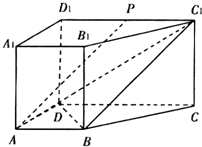 如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AD⊥AB,AB=AD=$\frac{1}{2}$CD=1.点P为线段C1D1的中点.
如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AD⊥AB,AB=AD=$\frac{1}{2}$CD=1.点P为线段C1D1的中点. 根据我国发布的《环境空气质量指数AQI技术规定》(试行),AQI共分为六级:[0,50)为优,[50,100)为良,[100,150)为轻度污染,[150,200)为重度污染,[200,250),[250,300)均为重度污染,300及以上为严重污染.某市2015年11月份30天的AQI的频率分布直方图如图所示.
根据我国发布的《环境空气质量指数AQI技术规定》(试行),AQI共分为六级:[0,50)为优,[50,100)为良,[100,150)为轻度污染,[150,200)为重度污染,[200,250),[250,300)均为重度污染,300及以上为严重污染.某市2015年11月份30天的AQI的频率分布直方图如图所示.