题目内容
5.已知函数f(x)=$\left\{\begin{array}{l}-{x^2}+2x,x≤0\\ ln(x+1),x>0\end{array}\right.$,若对x∈R都有|f(x)|≥ax,则实数a的取值范围是( )| A. | (-∞,0] | B. | [-2,0] | C. | [-2,1] | D. | (-∞,1] |
分析 作出函数的图象,利用不等式恒成立进行转化求解即可.
解答  解:由y=|f(x)|的图象知:
解:由y=|f(x)|的图象知:
①当x>0时,y=ax只有a≤0时,才有可能满足|f(x)|≥ax,可排除C,D.
②当x≤0时,y=|f(x)|=|-x2+2x|=x2-2x.
故由|f(x)|≥ax得x2-2x≥ax.
当x=0时,不等式为0≥0成立
当x<0时,不等式等价于x-2≤a.
∵x-2<-2,∴a≥-2.
综上可知:a∈[-2,0],
故选:B.
点评 本题主要考查不等式的应用,利用数形结合以及不等式恒成立进行转化是解决本题的关键.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
13.函数f(x)=tanωx(ω>0)的图象的相邻两支截直线y=1所得的线段长为$\frac{π}{4}$,则f($\frac{π}{12}$)的值是( )
| A. | 0 | B. | $\frac{\sqrt{3}}{3}$ | C. | 1 | D. | $\sqrt{3}$ |
16.不等式|x+1|-|x-5|<4的解集为( )
| A. | (-∞,4) | B. | (-∞,-4) | C. | (4,+∞) | D. | (-4,+∞) |
 根据我国发布的《环境空气质量指数AQI技术规定》(试行),AQI共分为六级:[0,50)为优,[50,100)为良,[100,150)为轻度污染,[150,200)为重度污染,[200,250),[250,300)均为重度污染,300及以上为严重污染.某市2015年11月份30天的AQI的频率分布直方图如图所示.
根据我国发布的《环境空气质量指数AQI技术规定》(试行),AQI共分为六级:[0,50)为优,[50,100)为良,[100,150)为轻度污染,[150,200)为重度污染,[200,250),[250,300)均为重度污染,300及以上为严重污染.某市2015年11月份30天的AQI的频率分布直方图如图所示.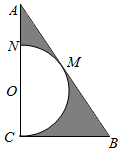 如图所示,△ABC中,∠C=90°,∠B=60°,AB=2$\sqrt{3}$,在三角形内挖去半圆(圆心O在边AC上,半圆与BC、AB相切于点C、M,与AC交于N),则图中阴影部分绕直线AC旋转一周所得旋转体的内外表面积之比为$\frac{4}{9}$.
如图所示,△ABC中,∠C=90°,∠B=60°,AB=2$\sqrt{3}$,在三角形内挖去半圆(圆心O在边AC上,半圆与BC、AB相切于点C、M,与AC交于N),则图中阴影部分绕直线AC旋转一周所得旋转体的内外表面积之比为$\frac{4}{9}$.