题目内容
已知函数f(x)=x3+ax2+bx+c
(1)若f(x)在x=-
和x=1时都取得极值,求实数a,b的值及函数f(x)的单调区间;
(2)若f(0)=0,f(1)=1,f(x)在(-2,
)上有极大值,求实数a的取值范围.
(1)若f(x)在x=-
| 2 |
| 3 |
(2)若f(0)=0,f(1)=1,f(x)在(-2,
| 1 |
| 4 |
考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:计算题,函数的性质及应用,导数的综合应用
分析:(1)求出f′(x)并令其为0得到方程,把x=-
和x=1代入求出a、b即可,再求出f′(x),分别令f′(x)<0,f′(x)>0,求出x的范围,即可得到函数f(x)的单调区间;
(2)由f(0)=0,f(1)=1,得到c=0,b=-a,再求f(x)的导数,由题意可得
,解不等式即可得到a的取值范围.
| 2 |
| 3 |
(2)由f(0)=0,f(1)=1,得到c=0,b=-a,再求f(x)的导数,由题意可得
|
解答:
解:(1)f′(x)=3x2+2ax+b,
由题意:
即
,
解得
,
即有f(x)=x3-
x2-2x+c,∴f′(x)=3x2-x-2,
令f′(x)<0,解得-
<x<1;
令f′(x)>0,解得x<-
或x>1,
∴f(x)的减区间为(-
,1);增区间为(-∞,-
),(1,+∞);
(2)若f(0)=0,f(1)=1,则c=0,1+a+b+c=1,则有b=-a,c=0,
则有f(x)=x3+ax2-ax,f′(x)=3x2+2ax-a,
由于f(x)在(-2,
)上有极大值,
即为
即
,
解得,
<a<
.
则实数a的取值范围为(
,
).
由题意:
|
|
解得
|
即有f(x)=x3-
| 1 |
| 2 |
令f′(x)<0,解得-
| 2 |
| 3 |
令f′(x)>0,解得x<-
| 2 |
| 3 |
∴f(x)的减区间为(-
| 2 |
| 3 |
| 2 |
| 3 |
(2)若f(0)=0,f(1)=1,则c=0,1+a+b+c=1,则有b=-a,c=0,
则有f(x)=x3+ax2-ax,f′(x)=3x2+2ax-a,
由于f(x)在(-2,
| 1 |
| 4 |
即为
|
|
解得,
| 3 |
| 8 |
| 12 |
| 5 |
则实数a的取值范围为(
| 3 |
| 8 |
| 12 |
| 5 |
点评:考查学生利用导数求函数极值的能力,利用导数研究函数单调性的能力,考查二次方程实根的分布,考查运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设i是虚数单位,复数
在复平面内表示的点在( )
| 10 |
| 3-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知命题p:若x>y,则-x<-y,q:?x0>0,(x0+1)e x0≤1,下列命题为真的是( )
| A、p∧q |
| B、(¬p)∨q |
| C、(¬p)∨(¬q) |
| D、p∨(¬q) |
已知函数f(x)=x3+ax2+bx+c.且0<f(-1)=f(-2)=f(-3)≤3,则( )
| A、c≤3 | B、3<c≤6 |
| C、6<c≤9 | D、c>9 |
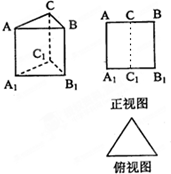 如图,水平放置的三棱柱的侧棱长和底边长均为2,且侧棱AA1⊥面A1B1C1,正视图是边长为2的正方形,俯视图为一个等边三角形,该三棱柱的左视图面积为( )
如图,水平放置的三棱柱的侧棱长和底边长均为2,且侧棱AA1⊥面A1B1C1,正视图是边长为2的正方形,俯视图为一个等边三角形,该三棱柱的左视图面积为( ) 如图,椭圆长轴端点为A,B,O为椭圆中心,F为椭圆的右焦点,
如图,椭圆长轴端点为A,B,O为椭圆中心,F为椭圆的右焦点,