题目内容
已知实数x，y满足
，则x2+y2+4x+6y+14的最大值为（ ）
|
| A、42 | ||
B、
| ||
C、
| ||
| D、46 |
考点：简单线性规划
专题：数形结合
分析：由约束条件作出可行域，化x2+y2+4x+6y+14为（x+2）2+（y+3）2+1，数形结合可得答案．
解答：
解：由约束条件
作可行域如图，
联立
，得B（3，1）．
联立
，得C（1，3）．
∵x2+y2+4x+6y+14=（x+2）2+（y+3）2+1．
点（-2，-3）与B的距离的平方为（3+2）2+（1+3）2=41．
点（-2，-3）与C的距离的平方为（1+2）2+（3+3）2=45．
∴x2+y2+4x+6y+14的最大值为46．
故选：D．
|
联立
|
联立
|
∵x2+y2+4x+6y+14=（x+2）2+（y+3）2+1．
点（-2，-3）与B的距离的平方为（3+2）2+（1+3）2=41．
点（-2，-3）与C的距离的平方为（1+2）2+（3+3）2=45．
∴x2+y2+4x+6y+14的最大值为46．
故选：D．
点评：本题考查了简单的线性规划，考查了数形结合的解题思想方法，是中档题．
练习册系列答案
相关题目
已知命题p：“若直线ax+y+1=0与直线ax-y+2=0垂直，则a=1”；命题q：“a
＞b
是a＞b”的充要条件，则（ ）
| 1 |
| 2 |
| 1 |
| 2 |
| A、p真q假 | B、p且q真 |
| C、p或q真 | D、p或q假 |
如图所示是一个几何体的三视图，则这个几何体外接球的表面积为（ ）
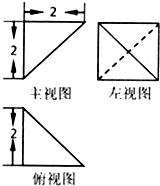
| A、8π | B、12π |
| C、16π | D、48π |
已知等差数列{an}的公差d≠0，Sn是其前n项和，若a22=a1a5，且a6+a9=5a3+3，则
的最大值是（ ）
| Sn |
| 2n |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
按照如图所示的算法框图，则输出的结果是（ ）
| A、1005 | B、1006 |
| C、1007 | D、1008 |
已知向量
的模为2
，
=（1，-2），条件p：向量
的坐标为（4，2），条件q：
⊥
，则p是q的（ ）
| a |
| 5 |
| b |
| a |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
如图，矩形ABCD所在的平面和平面ABEF互相垂直，等腰梯形ABEF中，AB∥EF，AB=2，AD=AF=1，∠BAF=60°，O，P分别为AB，CB的中点，M为底面△OBF的重心．