题目内容
2.已知函数f(x)=$\left\{\begin{array}{l}1-{x^2},x≥0\\ cosπx,x<0.\end{array}$若关于x的方程f(x+a)=0在(0,+∞)内有唯一实根,则实数a的最小值是-$\frac{1}{2}$.分析 作出f(x)的函数图象,根据函数图象得出a的范围即可得出答案.
解答 解:作出f(x)的函数图象如图所示:
∵f(x+a)在(0,+∞)上有唯一实根,
∴f(x)在(a,+∞)上有唯一实根,
∴-$\frac{1}{2}$≤a<1.
故答案为$-\frac{1}{2}$.
点评 本题考查了零点与函数图象的关系,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.已知圆C:x2+y2=1,点P为直线$\frac{x}{4}$+$\frac{y}{2}$=1上一动点,过点P向圆C引两条切线PA,PB,A,B为切点,则直线AB经过定点( )
| A. | $({\frac{1}{2},\frac{1}{4}})$ | B. | $({\frac{1}{4},\frac{1}{2}})$ | C. | $({\frac{{\sqrt{3}}}{4},0})$ | D. | $({0,\frac{{\sqrt{3}}}{4}})$ |
14.已知抛物线关于x轴对称,它的顶点在坐标原点O,焦点为F,并且经过点M(2,y0).若点M到该抛物线焦点的距离为3,则△MOF的面积为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |
11.已知tan(α-β)=$\frac{2}{3}$,tan($\frac{π}{6}$-β)=$\frac{1}{2}$,则tan(α-$\frac{π}{6}$)等于( )
| A. | $\frac{1}{4}$ | B. | $\frac{7}{8}$ | C. | $\frac{1}{8}$ | D. | $\frac{7}{9}$ |
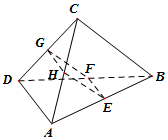 (文科)如图,在空间四面体ABCD中,若E,F,G,H分别是AB,BD,CD,AC的中点,
(文科)如图,在空间四面体ABCD中,若E,F,G,H分别是AB,BD,CD,AC的中点,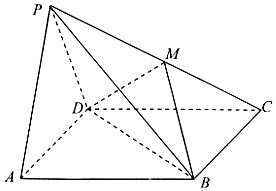 如图,四棱锥P-ABCD中,底面ABCD是矩形,平面PAD⊥底面ABCD,且△PAD是边长为2的等边三角形,PC=$\sqrt{13}$,M在PC上,且PA∥面MBD.
如图,四棱锥P-ABCD中,底面ABCD是矩形,平面PAD⊥底面ABCD,且△PAD是边长为2的等边三角形,PC=$\sqrt{13}$,M在PC上,且PA∥面MBD.