题目内容
3．设向量$\overrightarrow{a}$=（2，3），向量$\overrightarrow{b}$=（6，t），若$\overrightarrow{a}$与$\overrightarrow{b}$夹角为钝角，则实数t的取值范围为（-∞，-4）．分析 由题意可得$\overrightarrow{a}•\overrightarrow{b}$＜0，且$\overrightarrow{a}$、$\overrightarrow{b}$不共线，即$\left\{\begin{array}{l}{2×6+3t＜0}\\{\frac{6}{2}≠\frac{t}{3}}\end{array}\right.$，由此求得实数t的取值范围．
解答 解：若$\overrightarrow{a}$与$\overrightarrow{b}$夹角为钝角，向量$\overrightarrow{a}$=（2，3），向量$\overrightarrow{b}$=（6，t），
则$\overrightarrow{a}•\overrightarrow{b}$＜0，且$\overrightarrow{a}$、$\overrightarrow{b}$不共线，∴$\left\{\begin{array}{l}{2×6+3t＜0}\\{\frac{6}{2}≠\frac{t}{3}}\end{array}\right.$，求得t＜-4，
故答案为：（-∞，-4）．
点评 本题主要考查两个向量的数量公式，两个向量共线的性质，属于基础题．
练习册系列答案
相关题目
13．已知圆C：x2+y2=1，点P为直线$\frac{x}{4}$+$\frac{y}{2}$=1上一动点，过点P向圆C引两条切线PA，PB，A，B为切点，则直线AB经过定点（ ）
| A． | $（{\frac{1}{2}，\frac{1}{4}}）$ | B． | $（{\frac{1}{4}，\frac{1}{2}}）$ | C． | $（{\frac{{\sqrt{3}}}{4}，0}）$ | D． | $（{0，\frac{{\sqrt{3}}}{4}}）$ |
14．已知抛物线关于x轴对称，它的顶点在坐标原点O，焦点为F，并且经过点M（2，y0）．若点M到该抛物线焦点的距离为3，则△MOF的面积为（ ）
| A． | $\frac{{\sqrt{2}}}{2}$ | B． | $\sqrt{2}$ | C． | 2 | D． | $2\sqrt{2}$ |
11．已知tan（α-β）=$\frac{2}{3}$，tan（$\frac{π}{6}$-β）=$\frac{1}{2}$，则tan（α-$\frac{π}{6}$）等于（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{7}{8}$ | C． | $\frac{1}{8}$ | D． | $\frac{7}{9}$ |
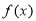，若对于定义域中的任意
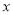，都有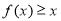
恒成立，则称函数
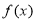为“爬坡函数”．
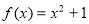是爬坡函数；
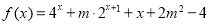是爬坡函数，求实数m的取值范围；
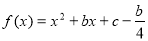都不是爬坡函数，求实数c的取值范围．