题目内容
 如图,将∠B=
如图,将∠B=| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
①AC⊥MN;
②DM与平面ABC所成的角是θ;
③线段MN的最大值是
| 3 |
| 4 |
| ||
| 4 |
④当θ=
| π |
| 2 |
| π |
| 2 |
其中正确的说法有
考点:与二面角有关的立体几何综合题
专题:空间位置关系与距离
分析:①连接BM,DM.则BM⊥AC,DM⊥AC,可得AC⊥平面BMD,即可得出AC⊥BD,即可判断出正误;
②由①可得:DM与平面ABC所成的角是θ或π-θ,即可判断出正误;
③BM=
,当θ=
时,MN取得最小值,MN=BMcos
;当θ=
时,MN取得最大值,MN=BMcos
,即可判断出正误;
④分别取AB,CD,CM的中点E,F,P,连接EM,MF,EF,EP,FP.则∠EMF或其补角是BC与AD所成的角,通过计算即可判断出正误.
②由①可得:DM与平面ABC所成的角是θ或π-θ,即可判断出正误;
③BM=
| ||
| 2 |
| 2π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
④分别取AB,CD,CM的中点E,F,P,连接EM,MF,EF,EP,FP.则∠EMF或其补角是BC与AD所成的角,通过计算即可判断出正误.
解答:
解:如图所示.
①连接BM,DM.则BM⊥AC,DM⊥AC,BM∩DM=M,∴AC⊥平面BMD,∴AC⊥BD,因此正确;
②由①可得:DM与平面ABC所成的角是θ或π-θ,因此不正确;
③BM=
,当θ=
时,MN取得最小值,MN=BMcos
=
,当θ=
时,MN取得最大值,MN=BMcos
=
,因此正确;
④分别取AB,CD,CM的中点E,F,P,连接EM,MF,EF,EP,FP.则∠EMF或其补角是BC与AD所成的角,∵FP=
DM=
,
EP2=(
)2+(
)2-2×
×
×cos120°=
,EP=
.∵FP⊥平面ABC,∴FP⊥EP,∴EF2=EP2+FP2=
,EM2+FM2=(
)2×2=
,∴EF2≠EM2+FM2,∴∠EMF≠
,因此不正确.
故答案为:①③.

①连接BM,DM.则BM⊥AC,DM⊥AC,BM∩DM=M,∴AC⊥平面BMD,∴AC⊥BD,因此正确;
②由①可得:DM与平面ABC所成的角是θ或π-θ,因此不正确;
③BM=
| ||
| 2 |
| 2π |
| 3 |
| π |
| 3 |
| ||
| 4 |
| π |
| 3 |
| π |
| 6 |
| 3 |
| 4 |
④分别取AB,CD,CM的中点E,F,P,连接EM,MF,EF,EP,FP.则∠EMF或其补角是BC与AD所成的角,∵FP=
| 1 |
| 2 |
| ||
| 4 |
EP2=(
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 7 |
| 16 |
| ||
| 4 |
| 10 |
| 16 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
故答案为:①③.
点评:本题考查了二面角的定义及其性质、线面垂直的判定与性质定理、三角形的中位线定理、勾股定理、余弦定理、空间角、菱形的性质,考查了空间想象能力,考查了推理能力与计算能力,属于难题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
已知一组数1,1,2,3,5,8,x,21,34,55,按这组数规律,x应为( )
| A、11 | B、12 | C、13 | D、14 |
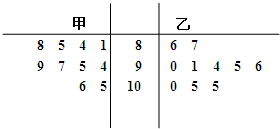 甲、乙两所学校高三级某学年10次联合考试的理科数学成绩平均分用茎叶图如图所示,则甲乙两所学校的平均分
甲、乙两所学校高三级某学年10次联合考试的理科数学成绩平均分用茎叶图如图所示,则甲乙两所学校的平均分. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|