题目内容
是否存在常数a,b,c,使得等式1(n2-12)+2(n2-22)+…+n(n2-n2)=an4+bn2+c对一切正整数n都成立?若存在,求出a,b,c的值;若不存在,说明理由.
考点:数学归纳法
专题:点列、递归数列与数学归纳法
分析:假设存在a,b,c,使得所给等式成立.通过n=1,2,3,列出方程组,求出abc即可.然后用数学归纳法证明等式1(n2-12)+2(n2-22)+…+n(n2-n2)=
n4-
n2对一切正整数n都成立.
| 1 |
| 4 |
| 1 |
| 4 |
解答:
解:假设存在a,b,c,使得所给等式成立.
令n=1,2,3代入等式得
,解得
以下用数学归纳法证明等式1(n2-12)+2(n2-22)+…+n(n2-n2)=
n4-
n2对一切正整数n都成立.
(1)当n=1时,由以上可知等式成立;
(2)假设当n=k时,等式成立,即1(k2-12)+2(k2-22)+…+k(k2-k2)=
k4-
k2,
则当n=k+1时,1[(k+1)2-12]+2[(k+1)2-22]+…+(k+1)[(k+1)2-(k+1)2]=
(k+1)4-
(k+1)2
=1(k2-12)+2(k2-22)+…+k(k2-k2)+(2k+1)+2(2k+1)+…+k(2k+1)
=
k4-
k2+(2k+1)
=
(k+1)4-
(k+1)2.
由(1)(2)知,等式结一切正整数n都成立.
令n=1,2,3代入等式得
|
|
以下用数学归纳法证明等式1(n2-12)+2(n2-22)+…+n(n2-n2)=
| 1 |
| 4 |
| 1 |
| 4 |
(1)当n=1时,由以上可知等式成立;
(2)假设当n=k时,等式成立,即1(k2-12)+2(k2-22)+…+k(k2-k2)=
| 1 |
| 4 |
| 1 |
| 4 |
则当n=k+1时,1[(k+1)2-12]+2[(k+1)2-22]+…+(k+1)[(k+1)2-(k+1)2]=
| 1 |
| 4 |
| 1 |
| 4 |
=1(k2-12)+2(k2-22)+…+k(k2-k2)+(2k+1)+2(2k+1)+…+k(2k+1)
=
| 1 |
| 4 |
| 1 |
| 4 |
| k(k+1) |
| 2 |
=
| 1 |
| 4 |
| 1 |
| 4 |
由(1)(2)知,等式结一切正整数n都成立.
点评:本题是探索性命题,它通过观察归纳、猜想、证明这一完整的思路过程去探索和发现问题,并证明所得结论的正确性,这是非常重要的一种思维能力.

练习册系列答案
相关题目
在等差数列{an}中,a2=2,a6=8,则a10的值为( )
| A、10 | B、12 | C、14 | D、16 |
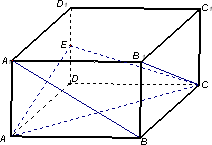 在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3,E是DD1的中点
在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3,E是DD1的中点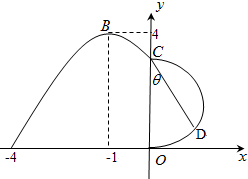 如图,某市新体育公园的中心广场平面图如图所示,在y轴左侧的观光道曲线段是函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<π),x∈[-4,0]时的图象且最高点B(-1,4),在y轴右侧的曲线段是以CO为直径的半圆弧.
如图,某市新体育公园的中心广场平面图如图所示,在y轴左侧的观光道曲线段是函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<π),x∈[-4,0]时的图象且最高点B(-1,4),在y轴右侧的曲线段是以CO为直径的半圆弧.