题目内容
已知|z1|=|z2|=|z1+z2|=1，则|z1-z2|等于 ．
考点：复数代数形式的乘除运算
专题：数系的扩充和复数
分析：不妨设z1=1，z2=cosθ+isinθθ∈[0，2π）．由于|z1+z2|=1，可得
=1，化为cosθ=-
．于是|z1-z2|=
，即可得出．
| (1+cosθ)2+sin2θ |
| 1 |
| 2 |
| (1-cosθ)2+sin2θ |
解答：
解：不妨设z1=1，z2=cosθ+isinθθ∈[0，2π）．
∵|z1+z2|=1，∴
=1，化为cosθ=-
．
则|z1-z2|=
=
=
．
故答案为：
．
∵|z1+z2|=1，∴
| (1+cosθ)2+sin2θ |
| 1 |
| 2 |
则|z1-z2|=
| (1-cosθ)2+sin2θ |
|
| 3 |
故答案为：
| 3 |
点评：本题考查了复数的运算法则和复数模的计算公式，属于中档题．
练习册系列答案
相关题目
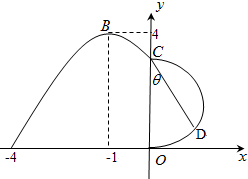如图，某市新体育公园的中心广场平面图如图所示，在y轴左侧的观光道曲线段是函数y=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π），x∈[-4，0]时的图象且最高点B（-1，4），在y轴右侧的曲线段是以CO为直径的半圆弧．