题目内容
已知：在三棱锥O-ABC中，OA⊥BC，OB⊥AC，求证：OC⊥AB．
考点：棱柱的结构特征,向量的数量积判断向量的共线与垂直
专题：计算题,空间位置关系与距离
分析：利用向量垂直的数量积公式，即可证明．
解答：
证明：∵OA⊥BC，∴
⊥
．
∵
•
=0，∴
•（
-
）=0，
∴
•
-
•
=0①
同理：由OB⊥AC得
•
-
•
=0②
由①-②得
•
-
•
=0，
∴
•（
-
）=0，
∴
•
=0，
∴
⊥
，
∴OC⊥AB．
| OA |
| BC |
∵
| OA |
| BC |
| OA |
| OC |
| OB |
∴
| OA |
| OC |
| OA |
| OB |
同理：由OB⊥AC得
| OB |
| OC |
| OB |
| OA |
由①-②得
| OA |
| OC |
| OB |
| OC |
∴
| OC |
| OA |
| OB |
∴
| OC |
| BA |
∴
| OC |
| BA |
∴OC⊥AB．
点评：本题考查向量的数量积判断向量的共线与垂直，考查学生的计算能力，比较基础．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
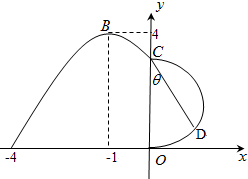如图，某市新体育公园的中心广场平面图如图所示，在y轴左侧的观光道曲线段是函数y=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π），x∈[-4，0]时的图象且最高点B（-1，4），在y轴右侧的曲线段是以CO为直径的半圆弧．