题目内容
已知定点F(2,0)与分别在x轴、y轴上的动点M(m,0)、N(0,n)满足:
•
=0,动点P满足
=
.
(1)求动点P的轨迹的方程;
(2)设过点F任作一直线与点P的轨迹交于A、B两点,直线OA、OB与直线l:x=-2分别交于点S、T(O为坐标原点);
(i)试判断直线l:x=-2与以AB为直径的圆的位置关系;
(ii)探究
•
是否为定值?并证明你的结论.
| MN |
| NF |
| MN |
| NP |
(1)求动点P的轨迹的方程;
(2)设过点F任作一直线与点P的轨迹交于A、B两点,直线OA、OB与直线l:x=-2分别交于点S、T(O为坐标原点);
(i)试判断直线l:x=-2与以AB为直径的圆的位置关系;
(ii)探究
| FS |
| FT |
考点:直线与圆锥曲线的综合问题,轨迹方程
专题:圆锥曲线中的最值与范围问题
分析:(1)设动点P的坐标为(x,y),由
•
=0,得n2+2m=0.由此利用(-m,n)=(x,y-n能求出动点P的轨迹方程.
(2)(i)设直线AB的方程为x=ty+2,点A,B的坐标分别为A(x1,y1),B(x2,y2).设A,B两点到准l:-2的距离分别为dA=|AF|,dB=|BF|,设AB的中点C到准线的距离为dC,由dC=
(dA+dB)能求出直线l:x=-2与以AB为直线的圆相切.
(ii)由
得y2-8ty-16=0,由已知条件分别求出S(-2,-
),T(-2,-
),由此能求出
•
为定值0.
| MN |
| NF |
(2)(i)设直线AB的方程为x=ty+2,点A,B的坐标分别为A(x1,y1),B(x2,y2).设A,B两点到准l:-2的距离分别为dA=|AF|,dB=|BF|,设AB的中点C到准线的距离为dC,由dC=
| 1 |
| 2 |
(ii)由
|
| 16 |
| y1 |
| 16 |
| y2 |
| FS |
| FT |
解答:
解:(1)设动点P的坐标为(x,y),则
=(x,y-n),
又
=(2,-n),
=(-m,n),由
•
=0,得n2+2m=0.
∵
=
,∴(-m,n)=(x,y-n),∴
,
代入n2+2m=0,得动点P的轨迹方程为y2=8x.
(2)由(1)知动点P的轨迹是以F(2,0)为焦点,l:x=-2为准线的抛物线,
设直线AB的方程为x=ty+2;点A,B的坐标分别为A(x1,y1),B(x2,y2).
(i)设A,B两点到准l:-2的距离分别为dA,dB,则dA=|AF|,dB=|BF|,
设AB的中点C到准线的距离为dC,
则dC=
(dA+dB)=
(|AF|+|BF|)=
|AB|,
∴直线l:x=-2与以AB为直线的圆相切.
(ii)由
得y2-8ty-16=0,∴y1y2=-16,…(10分)
∵OA的方程为y=
x,即y=
x,
由
,得点S的坐标为S(-2,-
),
同理可得点T的坐标为T(-2,-
),…(11分)
∴
=(-4,-
),
=(-4,-
),
于是
•
=16+
=16+
=0,…(12分)
因此
•
为定值,且定值为0.…(13分)
| NP |
又
| NF |
| MN |
| MN |
| NF |
∵
| MN |
| NP |
|
代入n2+2m=0,得动点P的轨迹方程为y2=8x.
(2)由(1)知动点P的轨迹是以F(2,0)为焦点,l:x=-2为准线的抛物线,
设直线AB的方程为x=ty+2;点A,B的坐标分别为A(x1,y1),B(x2,y2).
(i)设A,B两点到准l:-2的距离分别为dA,dB,则dA=|AF|,dB=|BF|,
设AB的中点C到准线的距离为dC,
则dC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴直线l:x=-2与以AB为直线的圆相切.
(ii)由
|
∵OA的方程为y=
| y1 |
| x1 |
| 8 |
| y1 |
由
|
| 16 |
| y1 |
同理可得点T的坐标为T(-2,-
| 16 |
| y2 |
∴
| FS |
| 16 |
| y1 |
| FT |
| 16 |
| y2 |
于是
| FS |
| FT |
| 16×16 |
| y1y2 |
| 16×16 |
| -16 |
因此
| FS |
| FT |
点评:本题考查动点的轨迹方程的求法,考查直线与圆的位置关系的判断,考查向量的数量积是否为定值的探究与证明,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
要得到函数y=cosx的图象,只需将函数y=sinx的图象沿x轴( )
A、向左平移
| ||
| B、向左平移π个长度单位 | ||
C、向右平移
| ||
| D、向右平移π个长度单位 |
在等差数列{an}中,a2=2,a6=8,则a10的值为( )
| A、10 | B、12 | C、14 | D、16 |
用二分法求方程f(x)=0在(1,2)内近似解的过程中得f(1)<0,f(1.5)>0,f(1.25)<0,则方程的根在区间( )
| A、(1.25,1.5) |
| B、(1,1.25) |
| C、(1.5,2) |
| D、不能确定 |
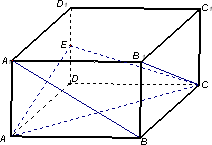 在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3,E是DD1的中点
在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3,E是DD1的中点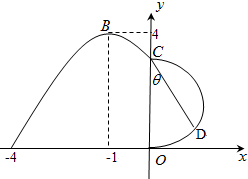 如图,某市新体育公园的中心广场平面图如图所示,在y轴左侧的观光道曲线段是函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<π),x∈[-4,0]时的图象且最高点B(-1,4),在y轴右侧的曲线段是以CO为直径的半圆弧.
如图,某市新体育公园的中心广场平面图如图所示,在y轴左侧的观光道曲线段是函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<π),x∈[-4,0]时的图象且最高点B(-1,4),在y轴右侧的曲线段是以CO为直径的半圆弧.