题目内容
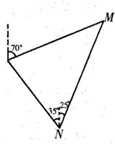 如图,一艘轮船从N处开始按照北偏西35°的方向以每小时30海里的速度航行,灯塔M原来在轮船的北偏东25°方向上,经过30分钟后,灯塔在轮船的北偏东70°方向上,则灯塔M距离N处的海里数为( )
如图,一艘轮船从N处开始按照北偏西35°的方向以每小时30海里的速度航行,灯塔M原来在轮船的北偏东25°方向上,经过30分钟后,灯塔在轮船的北偏东70°方向上,则灯塔M距离N处的海里数为( )A、
| ||||
B、
| ||||
C、30(
| ||||
D、30(
|
考点:解三角形的实际应用
专题:应用题,解三角形
分析:首先将实际问题抽象成解三角形问题,再借助于正弦定理求出边长.
解答:
 解:由题意可知△AMN中AN=15,∠N=60°,∠MAN=75°,
解:由题意可知△AMN中AN=15,∠N=60°,∠MAN=75°,
∴∠M=45°,由正弦定理可得
=
,
∴MN=
,
故选:A.
 解:由题意可知△AMN中AN=15,∠N=60°,∠MAN=75°,
解:由题意可知△AMN中AN=15,∠N=60°,∠MAN=75°,∴∠M=45°,由正弦定理可得
| 15 | ||||
|
| MN | ||||||
|
∴MN=
15(
| ||
| 2 |
故选:A.
点评:本题考查解三角形的实际应用,考查学生的计算能力,比较基础.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
不等式|x+2a|+|x-a|≥3对任意实数x都成立,则实数a的取值范围是( )
| A、(-∞,-3]∪[3,+∞) |
| B、(-∞,-1]∪[1,+∞) |
| C、[-3,3] |
| D、[-1,1] |
直角坐标系xoy中,以原点为极点,x轴的非负半轴为极轴建立极坐标系,已知圆C的极坐标方程为ρ=2sinθ,直线l的参数方程为
(t为参数),则圆C截直线l所得的弦长为( )
|
| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
为了得到函数y=cos(2x+1)的图象,只需将函数y=cos2x的图象上所有的点( )
A、向左平移
| ||
B、向右平移
| ||
| C、向左平移1个单位长度 | ||
| D、向右平移1个单位长度 |
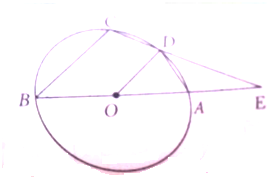 如图,BA是⊙O的直径,延长BA至E,使得AE=AO,过E点作⊙O的割线交⊙O于D、C,使得AD=DC.
如图,BA是⊙O的直径,延长BA至E,使得AE=AO,过E点作⊙O的割线交⊙O于D、C,使得AD=DC.