题目内容
18.已知p:-1≤x≤1,q:a≤ex≤b,其中a,b为实数.(1)若p是q的充要条件,求ab的值;
(2)若a=1,b=e2,且p,q中恰有一个为真命题,求实数x的范围.
分析 (1)可得a=e-1,b=e1,即ab=1.
(2)由题意得q:1≤ex≤e2,即q:0≤x≤2,
可得p,q中恰有一个为真命题,
分p真,q假; p假,q真求实数x的范围即可.
解答 解:(1)∵p:-1≤x≤1,且p是q的充要条件,
∴q等价于e-1≤ex≤e1,…(3分)
∴a=e-1,b=e1,∴ab=1. …(6分)
(2)由题意得q:1≤ex≤e2,即q:0≤x≤2,
∵p,q中恰有一个为真命题,…(7分)
当p真,q假时,
∴$\left\{{\begin{array}{l}{-1≤x≤1}\\{x<0或x>2}\end{array}}\right.$即-1≤x<0,…(9分)
当p假,q真时,
∴$\left\{{\begin{array}{l}{x<-1或x>1}\\{0≤x≤2}\end{array}}\right.$即1<x≤2,…(11分)
综上所述:实数x的范围为[-1,0)∪(1,2]. …(12分)
点评 本题考查了命题真假的应用,充要条件的应用,属于中档题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
13.命题?x∈R,ex-x-1≥0的否定是( )
| A. | ?x∈R,ex-x-1≤0 | B. | ?x0∈R,e${\;}^{{x}_{0}}$-x0-1≥0 | ||
| C. | ?x0∈R,e${\;}^{{x}_{0}}$-x0-1≤0 | D. | ?x0∈R,e${\;}^{{x}_{0}}$-x0-1<0 |
10.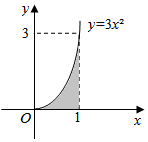 从如图所示的长方形区域内任取一个点M(x,y),则点M取自阴影部分的概率为( )
从如图所示的长方形区域内任取一个点M(x,y),则点M取自阴影部分的概率为( )
 从如图所示的长方形区域内任取一个点M(x,y),则点M取自阴影部分的概率为( )
从如图所示的长方形区域内任取一个点M(x,y),则点M取自阴影部分的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |