题目内容
2.已知函数f(x)=2x的反函数为y=g(x),(Ⅰ)若函数y=g(4-bx)在[1,+∞)上有最小值为3,求b的值;
(Ⅱ)若函数y=g(x)的图象经过点(6,a+1),且关于x的方程2ax-9x-m=0在区间[-1,1]上有解,求m的取值范围;
(Ⅲ)若函数h(x)=9x-k•3x+1(x≤0)有最小值-1,求k的值.
分析 由题意得g(x)=log2x.
(Ⅰ)y=g(4-bx)=log2(4-bx),令t=4-bx,由y=log2t在(0,+∞)上为增函数,得t=4-bx,在[1,+∞)上也应为增函数,且tmin=8,即可得出.
(Ⅱ)由f(x)=2x的图象经过点(a+1,6)得2a+1=6,可得2a=3,令h(x)=2ax-9x,可得$h(x)={3^x}-{9^x}=-{({3^x}-\frac{1}{2})^2}+\frac{1}{4}$,又x∈[-1,1],进而得出.
(Ⅲ)令t=3x(0<t≤1),$u(t)={t^2}+kt+1={(t+\frac{k}{2})^2}-\frac{k^2}{4}-1$,对k分类讨论即可得出.
解答 解:由题意得g(x)=log2x.
(Ⅰ)y=g(4-bx)=log2(4-bx),令t=4-bx,由y=log2t在(0,+∞)上为增函数,
得t=4-bx在[1,+∞)上也应为增函数,且tmin=8,即$\left\{\begin{array}{l}b<0\\ 4-b=8\end{array}\right.$得b=-4…(6分)
(Ⅱ)由f(x)=2x的图象经过点(a+1,6)得2a+1=6⇒2a=3,…(8分)
令h(x)=2ax-9x,则$h(x)={3^x}-{9^x}=-{({3^x}-\frac{1}{2})^2}+\frac{1}{4}$,
又x∈[-1,1],得${3^x}∈[{\frac{1}{3}\;,\;3}]$,(10分)
∴$h(x)∈[{-6\;,\;\frac{1}{4}}]$即$m∈[{-6\;,\;\frac{1}{4}}]$…(12分)
(Ⅲ)令t=3x(0<t≤1),$u(t)={t^2}+kt+1={(t+\frac{k}{2})^2}-\frac{k^2}{4}-1$
若$0<-\frac{k}{2}<1$时,即-2<k<0,$u{(t)_{min}}=u(-\frac{k}{2})=-\frac{k^2}{4}-1=-1$,得k=0,舍去;
若$-\frac{k}{2}≥1$时,即k≤-2,u(t)min=u(1)=-1,得k=-3.
综上,k=-3.
点评 本题考查了函数的单调性、换元法、不等式的解法,考查了推理能力与计算能力,属于中档题.

| A. | 24 | B. | 48 | C. | 60 | D. | 72 |
| A. | ?x∈R,ex-x-1≤0 | B. | ?x0∈R,e${\;}^{{x}_{0}}$-x0-1≥0 | ||
| C. | ?x0∈R,e${\;}^{{x}_{0}}$-x0-1≤0 | D. | ?x0∈R,e${\;}^{{x}_{0}}$-x0-1<0 |
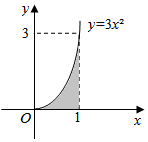 从如图所示的长方形区域内任取一个点M(x,y),则点M取自阴影部分的概率为( )
从如图所示的长方形区域内任取一个点M(x,y),则点M取自阴影部分的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
 在梯形ABCD中,$\overrightarrow{DC}$=2$\overrightarrow{AB}$=4$\overrightarrow{PC}$,且$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AD}$,则λ+μ的值为( )
在梯形ABCD中,$\overrightarrow{DC}$=2$\overrightarrow{AB}$=4$\overrightarrow{PC}$,且$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AD}$,则λ+μ的值为( )| A. | 1 | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |