题目内容
1．复数z满足|z-4i|-|z+4i|=4，则z在复平面上对应点的轨迹方程为$\frac{{y}^{2}}{4}-\frac{{x}^{2}}{12}=1$（y＜0）．分析 由|z-4i|-|z+4i|=4，得z在复平面上对应的点满足到（0，4）的距离减去到（0，-4）的距离为常数4，然后由双曲线定义得答案．
解答 解：由|z-4i|-|z+4i|=4，得
z在复平面上对应的点满足到（0，4）的距离减去到（0，-4）的距离为常数4，
则其轨迹是以（0，4）和（0，-4）为焦点得双曲线的下支，
其中2a=4，则a=2，2c=8，c=4，
∴b2=c2-a2=12，
∴轨迹方程为$\frac{{y}^{2}}{4}-\frac{{x}^{2}}{12}=1$（y＜0）．
故答案为：$\frac{{y}^{2}}{4}-\frac{{x}^{2}}{12}=1$（y＜0）．
点评 本题考查轨迹方程的求法，考查复数的代数表示法及其几何意义，是基础题．
练习册系列答案
相关题目
4．用数字1，2，3，4，5组成没有重复数字的五位数，其中偶数的个数为（ ）
| A． | 24 | B． | 48 | C． | 60 | D． | 72 |
8．在△ABC中，若b=1，c=$\sqrt{3}$，∠C=$\frac{2π}{3}$，则a等于（ ）
| A． | 2 | B． | $\sqrt{3}$ | C． | $\frac{1}{2}$ | D． | 1 |
13．命题?x∈R，ex-x-1≥0的否定是（ ）
| A． | ?x∈R，ex-x-1≤0 | B． | ?x0∈R，e${\;}^{{x}_{0}}$-x0-1≥0 | ||
| C． | ?x0∈R，e${\;}^{{x}_{0}}$-x0-1≤0 | D． | ?x0∈R，e${\;}^{{x}_{0}}$-x0-1＜0 |
10．
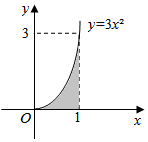从如图所示的长方形区域内任取一个点M（x，y），则点M取自阴影部分的概率为（ ）
从如图所示的长方形区域内任取一个点M（x，y），则点M取自阴影部分的概率为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{2}{3}$ |