题目内容

19．计算${∫}_{0}^{1}$（ex+1）dx=（　　）
A．2eB．e+1C．eD．e-1

分析 由题意首先求得原函数，然后利用微积分基本定理即可求得定积分的值．

解答 解：由微积分基本定理可得${∫}_{0}^{1}{（e}^{x}+1）dx=（{e}^{x}+x）{|}_{0}^{1}=（{e}^{1}+1）-（{e}^{0}+0）=e$．
故选：C．

点评 本题考查了定积分的计算，涉及的知识点包括微积分基本定理，基本初等函数的原函数，属于中档题．

练习册系列答案
相关题目
1．数列{an}中，a1=1，当n≥2时，${S_n}=\frac{3}{2}-{a_n}$，则an=$\left\{\begin{array}{l}{1，n=1}\\{（\frac{1}{2}）^{n}，n≥2}\end{array}\right.$．
10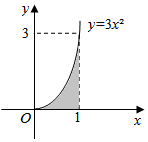．从如图所示的长方形区域内任取一个点M（x，y），则点M取自阴影部分的概率为（　　）
A．$\frac{1}{2}$B．$\frac{1}{4}$C．$\frac{1}{3}$D．$\frac{2}{3}$
7．函数f（x）=lg（a-x）+lgx（a＞0）的定义域为S，函数g（x）=$\sqrt{x}$+$\sqrt{2-x}$的定义域为T．
（1）若a=3，求S∪T和S∩T；
（2）若S⊆T，求a的取值范围．
14．已知函数f（x）=x3+mx2+nx-2的图象在点（-1，f（-1））处的切线方程为9x-y+3=0．
（1）求函数y=f（x）的解析式和单调区间；
（2）若函数f（x）（x∈[0，3]）的值域为A，函数f（x）（x∈[a，a+$\frac{3}{2}$]）的值域为B，当A⊆B时，求实数a的取值范围．
4．在平面直角坐标系xOy中，曲线y=x2-6x+1与坐标轴的交点都在圆C上．
（1）求圆C的方程；
（2）若圆C与直线x-y+a=0交于A，B两点，且OA⊥OB，求a的值．
7．已知函数y=f（x）是定义在[-5，0）∪（0，5]上的偶函数，且当x∈（0，5]时，f（x）=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}x（0＜x＜2）}\\{-{x}^{2}+8x-15（2≤x≤5）}\end{array}\right.$若函g（x）=f（x）-kx+2有三个不同的零点，则实数k的取值范围是（-8+2$\sqrt{13}$，-$\frac{2}{5}$]∪[$\frac{2}{5}$，8-2$\sqrt{13}$）．
4．已知a为实数，f（x）=（x2-4）（x-a）．
（1）若f′（-1）=0，求f（x）在[-2，2]上的最大值和最小值．
（2）若f（x）在[1，2]单调递增，求a的取值范围．
5．如图所示的是下列几个函数的图象：①y=ax； ②y=bx； ③y=cx； ④y=dx．则a，b，c，d与0和1的关系是（　　）
A．0＜a＜b＜1＜c＜dB．0＜b＜a＜1＜d＜cC．0＜b＜a＜1＜c＜dD．1＜a＜b＜c＜d

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网