题目内容
7.以平面直角坐标系xOy的原点为极点,x轴的非负半轴为极轴,取相同的长度单位建立极坐标系,曲线C在该极坐标系下的极坐标方程为ρ=4$\sqrt{2}$cos(θ+$\frac{π}{4}$).(1)求曲线C的直角坐标方程;
(2)设点P(x,y)在曲线C上,当x-y取得最小值时,求点P的极坐标.(ρ>0,0≤θ<2π)
分析 (1)曲线C的极坐标方程为ρ2=4ρcosθ+4ρsinθ,能求出曲线C的直角坐标方程.
(2)利用圆的参数方程得$x-y=2\sqrt{2}(cosα-sinα)$+4=4sin($α+\frac{3π}{4}$)+4,由此能求出当x-y取得最小值时点P的极坐标.
解答 解:(1)∵曲线C的极坐标方程为ρ=4$\sqrt{2}$cos(θ+$\frac{π}{4}$)=4cosθ-4sinθ,
∴ρ2=4ρcosθ-4ρsinθ,
∴x2+y2=4x-4y,即(x-2)2+(y+2)2=8.
(2)∵点P(x,y)在曲线C:(x-2)2+(y+2)2=8上,
∴$\left\{\begin{array}{l}{x=2+2\sqrt{2}cosα}\\{y=-2+2\sqrt{2}sinα}\end{array}\right.$,0≤α<2π.
∴$x-y=2\sqrt{2}(cosα-sinα)$+4=4sin($α+\frac{3π}{4}$)+4,
∴当$α+\frac{3π}{4}$=$\frac{3π}{2}$,$α=\frac{3π}{4}$时,x-y取最小值0,
此时$\left\{\begin{array}{l}{x=2+2\sqrt{2}×cos\frac{3π}{4}=0}\\{y=-2+2\sqrt{2}sin\frac{3π}{4}=0}\end{array}\right.$,∴P(0,0),
∴ρ=0,$θ=\frac{π}{2}$,∴点P的极坐标P(0,$\frac{π}{2}$).
点评 本题考查曲线的直角坐标方程的求法,考查点的极坐标的求法,是基础题,解题时要认真审题,注意极坐标和直角坐标互化公式的合理运用.

练习册系列答案
相关题目
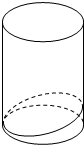 如图,用与圆柱的母线成60°角的平面截圆柱得到的截口曲线是椭圆,则该椭圆的离心率为$\frac{1}{2}$.
如图,用与圆柱的母线成60°角的平面截圆柱得到的截口曲线是椭圆,则该椭圆的离心率为$\frac{1}{2}$.