��Ŀ����
17�����������ĸ����⣺��������f��x��=logax��a��0��a��1�����䶨�������Ǽ���������loga2��0��
���躯��f��x��=2x+$\frac{1}{2x}$-1��x��0��������f��x������Сֵ1��
��������$\overrightarrow a=��1��k��$��$\overrightarrow b=��-2��6��$��$\overrightarrow{a}$��$\overrightarrow{b}$����k=-3��
�ܺ���y=��sinx+cosx��2-1����С��������2�У�
������ȷ���������Ǣ٢ۣ�
���� ���ö����������������a�ķ�Χ����һ����϶��������������жϢ٣����û�������ʽ��ú��������ֵ���ж���������Сֵ�жϢڣ������������ߵ������ʾ���k��ֵ�жϢۣ�ֱ����������������жϢܣ�
��� �⣺���ڢ٣�������f��x��=logax��a��0��a��1�����䶨�������Ǽ���������0��a��1����loga2��0���ʢ���ȷ��
���ڢڣ�����f��x��=2x+$\frac{1}{2x}$-1��x��0��=-[��-2x��+��$\frac{1}{-2x}$��]-1$��-2\sqrt{��-2x��•\frac{1}{-2x}}-1=-3$�����ҽ���x=-$\frac{1}{2}$ʱȡ��=����
�ຯ��f��x�������ֵ-3������Сֵ���ʢڴ���
���ڢۣ�������$\overrightarrow a=��1��k��$��$\overrightarrow b=��-2��6��$����$\overrightarrow{a}$��$\overrightarrow{b}$����1��6+2k=0�����k=-3���ʢ���ȷ��
���ڢܣ�����y=��sinx+cosx��2-1=1+2sinxcosx-1=sin2x������С�������ǦУ��ʢܴ���
����ȷ���������Ǣ٢ۣ�
�ʴ�Ϊ���٢ۣ�
���� ���⿼�����������ж���Ӧ�ã����麯�������ʣ�ѵ���˺�������ֵ�����ڵ������е��⣮

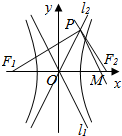 ��֪F1��F2�ֱ���˫����$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ��㣬l1��l2Ϊ˫���ߵ����������ߣ������M��b��0����ƽ����l1��ֱ�߽�l2�ڵ�P����PF1��PF2�����˫���ߵ�������Ϊ��������
��֪F1��F2�ֱ���˫����$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ��㣬l1��l2Ϊ˫���ߵ����������ߣ������M��b��0����ƽ����l1��ֱ�߽�l2�ڵ�P����PF1��PF2�����˫���ߵ�������Ϊ��������| A�� | $\sqrt{3}$ | B�� | $\sqrt{5}$ | C�� | $\frac{\sqrt{14-2\sqrt{41}}}{2}$ | D�� | $\frac{\sqrt{14+2\sqrt{41}}}{2}$ |
 ��ͼ��ʾ��AD��BC��EF��ƽ��ADFE��ƽ��BCFE��AE��EF��BE��EF��AD=AE=BE=2��EF=3��BC=4��GΪBC���е㣮
��ͼ��ʾ��AD��BC��EF��ƽ��ADFE��ƽ��BCFE��AE��EF��BE��EF��AD=AE=BE=2��EF=3��BC=4��GΪBC���е㣮