题目内容
12.斜率为1的动直线L与椭圆$\frac{x^2}{4}+\frac{y^2}{2}=1$交于P,Q两点,M是L上的点,且满足|MP|•|MQ|=2,求点M的轨迹方程.分析 设直线L的方程为:y=x+t,P(x1,y1),Q(x2,y2),M(m,n).可得y1=x1+t,y2=x2+t,t=n-m.直线方程与椭圆方程联立可得:3x2+4tx+2t2-4=0,|MP|=$\sqrt{({x}_{1}-m)^{2}+({y}_{1}-n)^{2}}$=$\sqrt{2({x}_{1}-m)^{2}}$,同理可得:|MQ|=$\sqrt{2({x}_{2}-m)^{2}}$.利用|MP|•|MQ|=2,代入化简即可得出.
解答 解:设直线L的方程为:y=x+t,P(x1,y1),Q(x2,y2),M(m,n).
则y1=x1+t,y2=x2+t,t=n-m.
联立$\left\{\begin{array}{l}{y=x+t}\\{{x}^{2}+2{y}^{2}=4}\end{array}\right.$,化为:3x2+4tx+2t2-4=0,
△=16t2-12(2t2-4)>0,解得:t2<6.∴x1+x2=-$\frac{4t}{3}$,${x}_{1}{x}_{2}=\frac{2{t}^{2}-4}{3}$.
|MP|=$\sqrt{({x}_{1}-m)^{2}+({y}_{1}-n)^{2}}$=$\sqrt{2({x}_{1}-m)^{2}}$,
同理可得:|MQ|=$\sqrt{2({x}_{2}-m)^{2}}$.
∵|MP|•|MQ|=2,∴1=|(x1-m)(x2-m)|=$|{x}_{1}{x}_{2}-m({x}_{1}+{x}_{2})+{m}^{2}|$,
∴m2+2n2=1或7.
∴点M的轨迹为椭圆,其方程为m2+2n2=1或7.
点评 本题考查了椭圆的标准方程及其性质、两点之间的距离公式、一元二次方程的根与系数的关系,考查了推理能力与计算能力,属于难题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| 参加书法班 | 未参加书法班 | |
| 参加演讲班 | 8 | 5 |
| 未参加演讲班 | 2 | 33 |
(II)在既参加书法班又参加演讲班的8名学员中,有5名男学员A1,A2,A3,A4,A5,3名女学员B1,B2,B3.现从这5名男学员和3名女学员中各随机选1人,求A1被选中且B1未被选中的概率.
 一个简单几何体的正视图、侧视图如图所示,则其俯视图不可能为:
一个简单几何体的正视图、侧视图如图所示,则其俯视图不可能为:①长方形;
②正方形;
③圆.
其中正确的是( )
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①② |
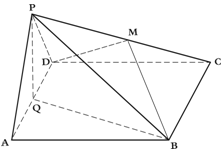 如图示,边长为4的正方形ABCD与正三角形ADP所在平面互相垂直,M、Q分别是PC,AD的中点.
如图示,边长为4的正方形ABCD与正三角形ADP所在平面互相垂直,M、Q分别是PC,AD的中点.