Question

1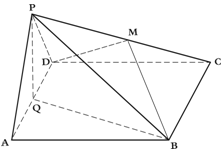．如图示，边长为4的正方形ABCD与正三角形ADP所在平面互相垂直，M、Q分别是PC，AD的中点．
（1）求证：PA∥面BDM
（2）求多面体P-ABCD的体积
（3）试问：在线段AB上是否存在一点N，使面PCN⊥面PQB？若存在，指出N的位置，若不存在，请说明理由．

Answer 1

分析 （1）连接AC交BD于点O，连接MO，由正方形ABCD知O为AC的中点，由M为PC的中点，知MO∥PA，由此能够证明PA∥平面MBD
（2）利用棱锥的体积公式，可得结论．
（3）存在点N，当N为AB中点时，平面PQB⊥平面PNC．由四边形ABCD是正方形，Q为AD的中点，知BQ⊥NC，由此能够证明平面PCN⊥平面PQB．

解答 （1）证明：连接AC交BD于点O，连接MO，
由正方形ABCD知O为AC的中点，
∵M为PC的中点，
∴MO∥PA，
∵MO?平面MBD，PA?平面MBD，
∴PA∥平面MBD
（2）解：多面体P-ABCD的体积=$\frac{1}{3}×\frac{1}{2}×4×4×2\sqrt{3}$=$\frac{16\sqrt{3}}{3}$；
（3）解：存在点N，当N为AB中点时，平面PQB⊥平面PNC，
∵四边形ABCD是正方形，Q为AD的中点，∴BQ⊥NC．
由（1）知，PQ⊥平面ABCD，NC?平面ABCD，∴PQ⊥NC，
又BQ∩PQ=Q，∴NC⊥平面PQB，
∵NC?平面PCN，
∴平面PCN⊥平面PQB．

点评 本题考查直线与平面平行的证明，考查四棱锥体积的求法，考查平面与平面垂直的证明，属于中档题．