题目内容
3.已知四组函数:①f(x)=1gx2,g(x)=2lgx;②f(x)=logaax,g(x)=${a}^{lo{g}_{a}x}$(a>0,a≠1);③f(x)=logaax(a>0,a≠1),g(x)=$\root{3}{{x}^{3}}$;④f(x)=$\frac{1}{x}$,g(x)=f-1(x).其中表示相同函数的序号是③④.分析 根据两个函数的定义域相同,对应关系也相同,即可判断它们是相同函数.
解答 解:对于①,f(x)=1gx2=2lg|x|的定义域是{x|x≠0},g(x)=2lgx的定义域是{x|x>0},定义域不同,对应关系也不同,不是同一函数;
对于②,f(x)=logaax=x的定义域是R,g(x)=${a}^{lo{g}_{a}x}$=x的定义域是{x|x>0},定义域不同,不是同一函数;
对于③,f(x)=logaax=x的定义域是R,g(x)=$\root{3}{{x}^{3}}$=x的定义域是R,定义域相同,对应关系也相同,是同一函数;
对于④,f(x)=$\frac{1}{x}$的定义域是{x|x≠0},g(x)=f-1(x)=$\frac{1}{x}$的定义域是{x≠0},定义域相同,对应关系也相同,是同一函数.
综上,表示相同函数的序号是③④.
故答案为:③④.
点评 本题考查了判断两个函数是否为同一函数的应用问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.棱长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,则线段D1E的长度为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
18.在△ABC中,角A,B,C所对的三边分别是a,b,c,已知$A={30°},c=2\sqrt{3},b=2$,则△ABC的面积为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
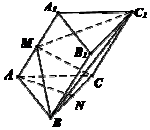 如图,在三棱锥ABC-A1B1C1中,AC=BC=AA1=2,∠ACB=90°,∠A1AC=60°,M,N分别是线段AA1,BC上的点,且NC=NB,AA1⊥平面BCM.
如图,在三棱锥ABC-A1B1C1中,AC=BC=AA1=2,∠ACB=90°,∠A1AC=60°,M,N分别是线段AA1,BC上的点,且NC=NB,AA1⊥平面BCM.