题目内容
6.在等比数列{an}中,(1)a2=3,a3=-6,求S6;
(2)a4=54,q=-3,求S5.
分析 根据等比数列的通项公式和等比数列的前n向和公式即可求出.
解答 解:(1)∵a2=3,a3=-6,
∴q=-2,a1=-$\frac{3}{2}$,
∴S6=$\frac{-\frac{3}{2}(1-(-2)^{6})}{1+2}$=25-$\frac{1}{2}$=$\frac{63}{2}$,
(2)a4=54,q=-3,
∴a1q3=a4,
∴a1(-3)3=54,
∴a1=-2,
∴S5=$\frac{-2(1-(-3)^{5})}{1+3}$=-122.
点评 本题考查了等比数列的通项公式和等比数列的前n项和公式,属于基础题.

练习册系列答案
相关题目
14.若2cos(θ-$\frac{π}{3}$)=3cosθ,则tanθ=( )
| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
18.若f(x)=2cos(2x+φ)(φ>0)的图象关于直线x=$\frac{π}{3}$对称,且当φ取最小值时,?x0∈(0,$\frac{π}{2}$),使得f(x0)=a,则a的取值范围是( )
| A. | (-1,2] | B. | [-2,-1) | C. | (-1,1) | D. | [-2,1) |
11.函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f(0)=( )
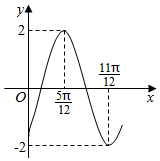

| A. | -$\sqrt{3}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | -1 | D. | -$\frac{1}{2}$ |
12.如果关于x的方程x2-ax+a2-3=0至少有一个正根,则实数a的取值范围是( )
| A. | -2<a<2 | B. | $\sqrt{3}<a≤2$ | C. | $-\sqrt{3}<a≤2$ | D. | $-\sqrt{3}≤a≤2$ |