题目内容
5.焦点在x轴上的椭圆$\frac{x^2}{3n}+{y^2}=1(n>0)$的焦距为$4\sqrt{2}$,则长轴长是( )| A. | 3 | B. | 6 | C. | $6\sqrt{2}$ | D. | 2 |
分析 求得椭圆的a,b,c,由题意可得3n>1,2c=$4\sqrt{2}$,解得n=3,即可得到所求值.
解答 解:椭圆$\frac{x^2}{3n}+{y^2}=1(n>0)$的a=$\sqrt{3n}$,b=1,c=$\sqrt{3n-1}$,
由题意可知$\left\{\begin{array}{l}3n>1\\ 2\sqrt{3n-1}=4\sqrt{2}\end{array}\right.⇒n=3$,
所以长轴长为2a=6,
故选:B.
点评 本题考查椭圆的方程和运用,主要考查椭圆的长轴长,注意运用a,b,c的关系,考查运算能力,属于基础题.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
15.已知复数Z的共轭复数$\overline{Z}$=$\frac{1-i}{1+2i}$,则复数Z的虚部是( )
| A. | $\frac{3}{5}$ | B. | $\frac{3}{5}$i | C. | -$\frac{3}{5}$ | D. | -$\frac{3}{5}$i |
13.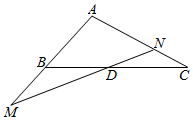 如图,在△ABC中,点D是BC上一点,且$\overrightarrow{BD}$=λ$\overrightarrow{DC}$,过点D的直线分别交直线AB、AC于不同的两点M、N,若$\overrightarrow{AB}$=$\frac{1}{2}$$\overrightarrow{AM}$,$\overrightarrow{AC}$=$\frac{3}{2}$$\overrightarrow{AN}$,则λ的值为( )
如图,在△ABC中,点D是BC上一点,且$\overrightarrow{BD}$=λ$\overrightarrow{DC}$,过点D的直线分别交直线AB、AC于不同的两点M、N,若$\overrightarrow{AB}$=$\frac{1}{2}$$\overrightarrow{AM}$,$\overrightarrow{AC}$=$\frac{3}{2}$$\overrightarrow{AN}$,则λ的值为( )
 如图,在△ABC中,点D是BC上一点,且$\overrightarrow{BD}$=λ$\overrightarrow{DC}$,过点D的直线分别交直线AB、AC于不同的两点M、N,若$\overrightarrow{AB}$=$\frac{1}{2}$$\overrightarrow{AM}$,$\overrightarrow{AC}$=$\frac{3}{2}$$\overrightarrow{AN}$,则λ的值为( )
如图,在△ABC中,点D是BC上一点,且$\overrightarrow{BD}$=λ$\overrightarrow{DC}$,过点D的直线分别交直线AB、AC于不同的两点M、N,若$\overrightarrow{AB}$=$\frac{1}{2}$$\overrightarrow{AM}$,$\overrightarrow{AC}$=$\frac{3}{2}$$\overrightarrow{AN}$,则λ的值为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
14.若2cos(θ-$\frac{π}{3}$)=3cosθ,则tanθ=( )
| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
11.函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f(0)=( )
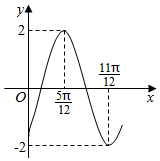

| A. | -$\sqrt{3}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | -1 | D. | -$\frac{1}{2}$ |
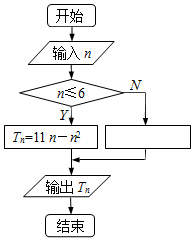 已知{an}是递减等差数列,如图是对数列{|an|}前n项和Tn求法的算法流程图,图中空白处理框中应填入${T_n}={n^2}-11n+60$.
已知{an}是递减等差数列,如图是对数列{|an|}前n项和Tn求法的算法流程图,图中空白处理框中应填入${T_n}={n^2}-11n+60$.