Question

已知变量x，y满足约束条件

x+y≥1 y≤4 x-y≤1

，若z=kx+y的最大值为5，则实数k=

 

．

Answer 1

考点：简单线性规划

专题：不等式的解法及应用

分析：作出不等式组对应的平面区域，利用目标函数的几何意义，利用数形结合即可得到结论．

解答： 解：作出不等式组对应的平面区域如图：
由z=kx+y得y=-kx+z，
∴直线的截距最大，对应的z也取得最大值，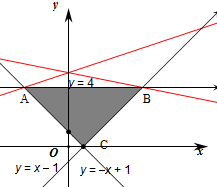
即平面区域在直线y=-kx+z的下方，
若-k＜0，平移直线y=-kx+z，由图象可知当直线y=-kx+z经过点B时，直线y=-kx+z的截距最大，此时z最大为5，
即kx+y=5
由

y=4 y=x-1

，解得

x=5 y=4

，
即B（5，4），
此时5k+4=5，解得k=

1

5

，
若-k＞0，平移直线y=-kx+z，由图象可知当直线y=-kx+z经过点A时，直线y=-kx+z的截距最大，此时z最大为5，
即kx+y=5
由

y=4 y=-x+1

，解得

x=-3 y=4

，
即A（-3，4），
此时-3k+4=5，解得k=-

1

3

故答案为：-

1

3

或

1

5

点评：本题主要考查线性规划的应用，利用z的几何意义，结合数形结合是解决本题的关键．