题目内容
设F1,F2为双曲线C:
-
=1(a>0)的左、右焦点,点P为双曲线C上一点,如果||PF1|-|PF2||=4,那么双曲线C的方程为 ;离心率为 .
| x2 |
| a2 |
| y2 |
| 16 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:求出双曲线的b=4,由双曲线的定义可得a=2,进而得到双曲线方程,由a,b,c的关系求得c,再由离心率公式计算即可得到.
解答:
解:双曲线C:
-
=1(a>0)的b=4,
由双曲线的定义,可得,||PF1|-|PF2||=2a=4,
即a=2,c=
=2
.
则双曲线的方程为
-
=1,
离心率e=
=
.
故答案为:
-
=1,
.
| x2 |
| a2 |
| y2 |
| 16 |
由双曲线的定义,可得,||PF1|-|PF2||=2a=4,
即a=2,c=
| a2+b2 |
| 5 |
则双曲线的方程为
| x2 |
| 4 |
| y2 |
| 16 |
离心率e=
| c |
| a |
| 5 |
故答案为:
| x2 |
| 4 |
| y2 |
| 16 |
| 5 |
点评:本题考查双曲线的定义、方程和性质,考查离心率的求法,属于基础题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
如果执行图中的程序框图,那么最后输出的正整数i=( )


| A、43 | B、44 | C、45 | D、46 |
 甲、乙两位同学在相同的5次数学测试中,测试成绩如图所示,设
甲、乙两位同学在相同的5次数学测试中,测试成绩如图所示,设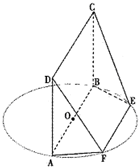 AB为圆O的直径,点E、F在圆上,AB∥EF,矩形ABCD所在平面与圆O所在平面互相垂直,已知AB=2,BC=EF=1.
AB为圆O的直径,点E、F在圆上,AB∥EF,矩形ABCD所在平面与圆O所在平面互相垂直,已知AB=2,BC=EF=1.