题目内容
已知函数f（x）对于任意的x、y∈R，都有f（x）•f（y）-f（xy）=3x+3y+6，则f（2008）= ．
考点：抽象函数及其应用,函数的值
专题：计算题,函数的性质及应用
分析：由条件，令x=y=1，得f（1）=4或-3，令x=y=0，得，f（0）=3或-2，令x=1，y=0，则f（1）•f（0）-f（0）=9，代入f（0）和f（1），发现f（1）=4，f（0）=3成立，再令x=2008，y=1，即可得到所求．
解答：
解：对于任意的x、y∈R，都有f（x）•f（y）-f（xy）=3x+3y+6，
令x=y=1，则f（1）•f（1）-f（1）=12，
解得，f（1）=4或-3，
令x=y=0，则f（0）•f（0）-f（0）=6，
解得，f（0）=3或-2，
令x=1，y=0，则f（1）•f（0）-f（0）=9，
代入f（0）和f（1），发现f（1）=4，f（0）=3成立，
则令x=2008，y=1，得f（2008）•f（1）-f（2008）=3×2008+3+6，
解得，f（2008）=2011，
故答案为：2011．
令x=y=1，则f（1）•f（1）-f（1）=12，
解得，f（1）=4或-3，
令x=y=0，则f（0）•f（0）-f（0）=6，
解得，f（0）=3或-2，
令x=1，y=0，则f（1）•f（0）-f（0）=9，
代入f（0）和f（1），发现f（1）=4，f（0）=3成立，
则令x=2008，y=1，得f（2008）•f（1）-f（2008）=3×2008+3+6，
解得，f（2008）=2011，
故答案为：2011．
点评：本题考查抽象函数及运用，考查抽象函数值的求法：赋值法，正确赋值是迅速解题的关键，考查运算能力，属于中档题．
练习册系列答案
相关题目
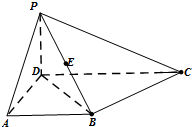如图，在四棱椎P-ABCD中，PD⊥平面ABCD，CD∥AB，CD⊥DA且PD=DA=AB=
已知抛物线C：x2=2py（p＞0）的焦点为F，点A（a，4）为抛物线C上的定点，点P为抛物线C上的动点．且△FOA的外接圆圆心到准线的距离为