题目内容
已知m,n表示两条直线,α,β,γ表示三个平面,则下列是真命题的有( )个.
①若α∩γ=m,β∩γ=n,m∥n,则α∥β;
②若m,n相交且都在α,β外,m∥α,m∥β,n∥α,n∥β,则α∥β;
③若m∥α,m∥β,则α∥β;
④m∥α,n∥β,m∥n,则α∥β.
①若α∩γ=m,β∩γ=n,m∥n,则α∥β;
②若m,n相交且都在α,β外,m∥α,m∥β,n∥α,n∥β,则α∥β;
③若m∥α,m∥β,则α∥β;
④m∥α,n∥β,m∥n,则α∥β.
| A、1 | B、2 | C、3 | D、4 |
考点:命题的真假判断与应用
专题:阅读型,空间位置关系与距离
分析:对于①,比如三棱柱的三个侧面,两两相交,且侧棱平行,即可判断;
对于②,可由面面平行的判定定理即可判断;
对于③,可考虑m和交线平行,即可判断;
对于④,可考虑m、n和交线平行,即可判断.
对于②,可由面面平行的判定定理即可判断;
对于③,可考虑m和交线平行,即可判断;
对于④,可考虑m、n和交线平行,即可判断.
解答:
解:对于①,比如三棱柱的三个侧面,两两相交,且侧棱平行,满足条件,但它们不平行,故①错;
对于②,若m,n相交且都在α,β外,m∥α,m∥β,n∥β,n∥α,
由面面平行的判定定理可得,设m,n相交确定的平面为γ,则有γ∥α,γ∥β,
则有α∥β,故②对;
对于③,若m∥α,m∥β,则α∥β或α、β相交,由于m可和交线平行,故③错;
对于④,若m∥α,n∥β,m∥n,则α∥β或α、β相交,由于m、n可和交线平行,故④错.
故选A.
对于②,若m,n相交且都在α,β外,m∥α,m∥β,n∥β,n∥α,
由面面平行的判定定理可得,设m,n相交确定的平面为γ,则有γ∥α,γ∥β,
则有α∥β,故②对;
对于③,若m∥α,m∥β,则α∥β或α、β相交,由于m可和交线平行,故③错;
对于④,若m∥α,n∥β,m∥n,则α∥β或α、β相交,由于m、n可和交线平行,故④错.
故选A.
点评:本题考查空间直线与平面的位置关系,考查线面平行的判断和性质,以及面面平行的判断和性质,考查空间想象能力,以及推理能力,属于基础题和易错题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
阅读如图程序框图,输出的结果是( )

| A、i=3 | B、i=4 |
| C、i=5 | D、i=6 |
已知等比数列{an}满足a1+a2=10,a2+a3=15,则an=( )
A、4×(
| ||
B、4×(
| ||
C、4×(
| ||
D、4×(
|
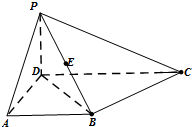 如图,在四棱椎P-ABCD中,PD⊥平面ABCD,CD∥AB,CD⊥DA且PD=DA=AB=
如图,在四棱椎P-ABCD中,PD⊥平面ABCD,CD∥AB,CD⊥DA且PD=DA=AB= 如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为棱DD1和AB上的点,则下列说法正确的是
如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为棱DD1和AB上的点,则下列说法正确的是