题目内容
设圆C1的方程为(x-2)2+(y-3m)2=4m2,直线l的方程为y=x+m-1.
(Ⅰ)求C1关于l对称的圆C2的方程;
(Ⅱ)当m变化且m≠0时,求证:C2的圆心在一条定直线上,并求C2所表示的一系列圆的公切线方程.
(Ⅰ)求C1关于l对称的圆C2的方程;
(Ⅱ)当m变化且m≠0时,求证:C2的圆心在一条定直线上,并求C2所表示的一系列圆的公切线方程.
考点:直线与圆相交的性质
专题:直线与圆
分析:(Ⅰ) 由圆的方程找出圆心坐标,设出圆心关于直线l的对称点的坐标,由直线l的斜率,根据两直线垂直时斜率的乘积为-1求出直线C1C2的斜率,由圆心及对称点的坐标表示出斜率,等于求出的斜率列出一个关系式,然后利用中点坐标公式,求出两圆心的中点坐标,代入直线l的方程,得到另一个关系式,两关系式联立即可用m表示出a与b,把表示出的a与b代入圆C2的方程即可;
(Ⅱ)由表示出的a与b消去m,得到a与b的关系式,进而得到圆C2的圆心在定直线上;分公切线的斜率不存在和存在两种情况考虑,当公切线斜率不存在时,容易得到公切线方程为x=0;当公切线斜率存在时,设直线y=kx+b与圆系中的所有圆都相切,根据点到直线的距离公式表示出圆心(a,b)到直线y=kx+b的距离d,当d等于圆的半径2|m|,化简后根据多项式为0时各项的系数为0,即可求出k与b的值,从而确定出C2所表示的一系列圆的公切线方程,这样得到所有C2所表示的一系列圆的公切线方程.
(Ⅱ)由表示出的a与b消去m,得到a与b的关系式,进而得到圆C2的圆心在定直线上;分公切线的斜率不存在和存在两种情况考虑,当公切线斜率不存在时,容易得到公切线方程为x=0;当公切线斜率存在时,设直线y=kx+b与圆系中的所有圆都相切,根据点到直线的距离公式表示出圆心(a,b)到直线y=kx+b的距离d,当d等于圆的半径2|m|,化简后根据多项式为0时各项的系数为0,即可求出k与b的值,从而确定出C2所表示的一系列圆的公切线方程,这样得到所有C2所表示的一系列圆的公切线方程.
解答:
解:(Ⅰ)∵圆C1的方程为(x-2)2+(y-3m)2=4m2,
∴圆心为(2,3m),设它关于直线l:y=x+m-1的对称点为(a,b),
则
,
解得a=2m+1,b=m+1,
∴圆C2的圆心为(2m+1,m+1),
∴圆C2的方程为:(x-2m-1)2+(y-m-1)2=4m2,
∴C1关于l对称的圆C2的方程:(x-2m-1)2+(y-m-1)2=4m2.
(Ⅱ)根据(Ⅰ) 得
圆C2的圆心为(2m+1,m+1),
令
,消去m得
x-2y+1=0,
它表示一条直线,
故C2的圆心在一条定直线上,
①当公切线的斜率不存在时,易求公切线的方程为x=0;
②当公切线的斜率存在时,设直线y=kx+b与圆系中的所有圆都相切,
∴
=2|m|,
即:(1-4k)m2+2(2k-1)(k+b-1)m+(k+b-1)2=0
∵直线y=kx+b与圆系中的所有圆都相切,所以上述方程对所有的m值都成立,
∴所以有:
,
解得
,
∴C2所表示的一系列圆的公切线方程为:y=
x+
,
∴故所求圆的公切线为x=0或y=
x+
.
∴圆心为(2,3m),设它关于直线l:y=x+m-1的对称点为(a,b),
则
|
解得a=2m+1,b=m+1,
∴圆C2的圆心为(2m+1,m+1),
∴圆C2的方程为:(x-2m-1)2+(y-m-1)2=4m2,
∴C1关于l对称的圆C2的方程:(x-2m-1)2+(y-m-1)2=4m2.
(Ⅱ)根据(Ⅰ) 得
圆C2的圆心为(2m+1,m+1),
令
|
x-2y+1=0,
它表示一条直线,
故C2的圆心在一条定直线上,
①当公切线的斜率不存在时,易求公切线的方程为x=0;
②当公切线的斜率存在时,设直线y=kx+b与圆系中的所有圆都相切,
∴
| |k•(2m+1)-(m+1)+b| | ||
|
即:(1-4k)m2+2(2k-1)(k+b-1)m+(k+b-1)2=0
∵直线y=kx+b与圆系中的所有圆都相切,所以上述方程对所有的m值都成立,
∴所以有:
|
解得
|
∴C2所表示的一系列圆的公切线方程为:y=
| 1 |
| 4 |
| 3 |
| 4 |
∴故所求圆的公切线为x=0或y=
| 1 |
| 4 |
| 3 |
| 4 |
点评:此题考查了直线与圆的位置关系,以及关于点与直线对称的圆的方程.此题的综合性比较强,要求学生审清题意,综合运用方程与函数的关系,掌握直线与圆相切时圆心到直线的距离等于半径,在作(Ⅱ)时先用消去参数的方法求定直线的方程,然后采用分类讨论的数学思想分别求出C2所表示的一系列圆的公切线方程.

练习册系列答案
相关题目
若数列{an}是等比数列,a2=1,其前n项和为Sn,则S3的取值范围是( )
| A、(-∞,1] |
| B、(-∞,0)∪(1,+∞) |
| C、[3,+∞) |
| D、(-∞,-1]∪[3,+∞) |
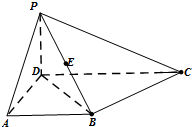 如图,在四棱椎P-ABCD中,PD⊥平面ABCD,CD∥AB,CD⊥DA且PD=DA=AB=
如图,在四棱椎P-ABCD中,PD⊥平面ABCD,CD∥AB,CD⊥DA且PD=DA=AB= 已知抛物线C:x2=2py(p>0)的焦点为F,点A(a,4)为抛物线C上的定点,点P为抛物线C上的动点.且△FOA的外接圆圆心到准线的距离为
已知抛物线C:x2=2py(p>0)的焦点为F,点A(a,4)为抛物线C上的定点,点P为抛物线C上的动点.且△FOA的外接圆圆心到准线的距离为