题目内容
10.已知函数f(x)=$\frac{x}{{e}^{x}}$,定义f1(x)=f′(x),f2(x)=[f1(x)]′,…,fn+1(x)=[fn(x)]′,n∈N,则fn(x)=$\frac{{{{(-1)}^n}(x-n)}}{e^x}$.分析 求函数的导数,根据导数的公式,寻找规律,利用归纳推理进行求解即可.
解答 解:∵f1(x)=$\frac{1-x}{{e}^{x}}$=$\frac{{(-1)}^{1}(x-1)}{{e}^{x}}$,
f2(x)=$\frac{x-2}{{e}^{x}}$=$\frac{{(-1)}^{2}(x-2)}{{e}^{x}}$,
f3(x)=$\frac{3-x}{{e}^{x}}$=$\frac{{(-1)}^{3}(x-3)}{{e}^{x}}$,
…,
由此归纳可得:fn(x)=$\frac{{{{(-1)}^n}(x-n)}}{e^x}$,
故答案为:$\frac{{{{(-1)}^n}(x-n)}}{e^x}$.
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
相关题目
1.已知抛物线y2=4x的焦点为F,定点P(4,-2),在抛物线上找一点M,使得|PM|+|MF|最小,则点M的坐标为( )
| A. | (2,-2) | B. | (1,2) | C. | (1,-2) | D. | (-1,2) |
18.某单位有496名职工,其中青年人有271名,中年人有178名,老年人有47名,为了了解该单位职工身体状况,抽取一个容量为n的样本进行统计分析,如表是根据抽取的样本数据(均为整数,单位:分)制作的频率分布表:
(1)采用分层抽样,在青年人、中年人和老年人中应各抽取多少人?
(2)试根据表中数据完成频率分布表(直接填写在在表格中);
(3)若数据在区间[59.5,74.5)的职工的身体处于亚健康状态,试问该单位约有多少名职工处于亚健康状态?
频率分布表
(1)采用分层抽样,在青年人、中年人和老年人中应各抽取多少人?
(2)试根据表中数据完成频率分布表(直接填写在在表格中);
(3)若数据在区间[59.5,74.5)的职工的身体处于亚健康状态,试问该单位约有多少名职工处于亚健康状态?
频率分布表
| 分组 | 频数 | 频率 |
| (49.5,59.5) | 12 | 0.24 |
| (59.5,69.5) | 16 | 0.32 |
| (69.5,79.5) | 10 | |
| (79.5,89.5) | 0.16 | |
| (89.5,99.5) | ||
| 合计 |
2.若三角形两内角α,β满足sinα•cosβ>0,则此三角形为( )
| A. | 钝角三角形 | B. | 直角三角形 | C. | 锐角三角形 | D. | 不确定 |
10.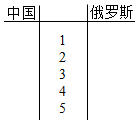 第31届夏季奥林匹克运动会将于2016年8月5日-21日在巴西里约热内卢举行.下表是近五届奥运会中国代表团和俄罗斯代表团获得的金牌数的统计数据(单位:枚).
第31届夏季奥林匹克运动会将于2016年8月5日-21日在巴西里约热内卢举行.下表是近五届奥运会中国代表团和俄罗斯代表团获得的金牌数的统计数据(单位:枚).
(Ⅰ)根据表格中两组数据完成近五届奥运会两国代表团获得的金牌数的茎叶图,并通过茎叶图比较两国代表团获得的金牌数的平均值及分散程度(不要求计算出具体数值,给出结论即可);
(Ⅱ)甲、乙、丙三人竞猜今年中国代表团和俄罗斯代表团中的哪一个获得的金牌数多(假设两国代表团获得的金牌数不会相等),规定甲、乙、丙必须在两个代表团中选一个,已知甲、乙猜中国代表团的概率都为$\frac{4}{5}$,丙猜中国代表团的概率为$\frac{3}{5}$,三人各自猜哪个代表团的结果互不影响.现让甲、乙、丙各猜一次,设三人中猜中国代表团的人数为X,求X的分布列及数学期望EX.
 第31届夏季奥林匹克运动会将于2016年8月5日-21日在巴西里约热内卢举行.下表是近五届奥运会中国代表团和俄罗斯代表团获得的金牌数的统计数据(单位:枚).
第31届夏季奥林匹克运动会将于2016年8月5日-21日在巴西里约热内卢举行.下表是近五届奥运会中国代表团和俄罗斯代表团获得的金牌数的统计数据(单位:枚).| 第30届伦敦 | 第29届北京 | 第28届雅典 | 第27届悉尼 | 第26届亚特兰大 | |
| 中国 | 38 | 51 | 32 | 28 | 16 |
| 俄罗斯 | 24 | 23 | 27 | 32 | 26 |
(Ⅱ)甲、乙、丙三人竞猜今年中国代表团和俄罗斯代表团中的哪一个获得的金牌数多(假设两国代表团获得的金牌数不会相等),规定甲、乙、丙必须在两个代表团中选一个,已知甲、乙猜中国代表团的概率都为$\frac{4}{5}$,丙猜中国代表团的概率为$\frac{3}{5}$,三人各自猜哪个代表团的结果互不影响.现让甲、乙、丙各猜一次,设三人中猜中国代表团的人数为X,求X的分布列及数学期望EX.