题目内容
10. 第31届夏季奥林匹克运动会将于2016年8月5日-21日在巴西里约热内卢举行.下表是近五届奥运会中国代表团和俄罗斯代表团获得的金牌数的统计数据(单位:枚).
第31届夏季奥林匹克运动会将于2016年8月5日-21日在巴西里约热内卢举行.下表是近五届奥运会中国代表团和俄罗斯代表团获得的金牌数的统计数据(单位:枚).| 第30届伦敦 | 第29届北京 | 第28届雅典 | 第27届悉尼 | 第26届亚特兰大 | |
| 中国 | 38 | 51 | 32 | 28 | 16 |
| 俄罗斯 | 24 | 23 | 27 | 32 | 26 |
(Ⅱ)甲、乙、丙三人竞猜今年中国代表团和俄罗斯代表团中的哪一个获得的金牌数多(假设两国代表团获得的金牌数不会相等),规定甲、乙、丙必须在两个代表团中选一个,已知甲、乙猜中国代表团的概率都为$\frac{4}{5}$,丙猜中国代表团的概率为$\frac{3}{5}$,三人各自猜哪个代表团的结果互不影响.现让甲、乙、丙各猜一次,设三人中猜中国代表团的人数为X,求X的分布列及数学期望EX.
分析 (Ⅰ)作出两国代表团获得的金牌数的茎叶图,通过茎叶图可以看出,中国代表团获得的金牌数的平均值高于俄罗斯代表团获得的金牌数的平均值,俄罗斯代表团获得的金牌数比较集中,中国代表团获得的金牌数比较分散.
(Ⅱ)由已知得X的可能取值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列和EX.
解答 解:(Ⅰ)两国代表团获得的金牌数的茎叶图如下
通过茎叶图可以看出,中国代表团获得的金牌数的平均值高于俄罗斯代表团获得的金牌数的平均值;
俄罗斯代表团获得的金牌数比较集中,中国代表团获得的金牌数比较分散.…(6分)
(Ⅱ)由已知得X的可能取值为0,1,2,3,
设事件A、B、C分别表示甲、乙、丙猜中国代表团,
则P(X=0)=P($\overline{A}$)P($\overline{B}$)P($\overline{C}$)=(1-$\frac{4}{5}$)2(1-$\frac{3}{5}$)=$\frac{2}{125}$,
P(X=1)=$P(A\overline{B}\overline{C})+P(\overline{A}B\overline{C})+P(\overline{A}\overline{B}C)$
=${C}_{2}^{1}×\frac{4}{5}×(1-\frac{4}{5})(1-\frac{3}{5})$+(1-$\frac{4}{5}$)2×$\frac{3}{5}$=$\frac{19}{125}$,
P(X=2)=$P(AB\overline{C})+P(A\overline{B}C)+P(\overline{A}BC)$
=($\frac{4}{5}$)2(1-$\frac{3}{5}$)+C${\;}_{2}^{1}$($\frac{4}{5}$)(1-$\frac{4}{5}$)($\frac{3}{5}$)=$\frac{56}{125}$,
P(X=3)=P(A)P(B)P(C)=($\frac{4}{5}$)2($\frac{3}{5}$)=$\frac{48}{125}$,
故X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{2}{125}$ | $\frac{19}{125}$ | $\frac{56}{125}$ | $\frac{48}{125}$ |
EX=$0×\frac{2}{125}+1×\frac{19}{125}+2×\frac{56}{125}+3×\frac{48}{125}$=$\frac{11}{5}$.…(12分)
点评 本题考查茎顺图的作法及应用,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意对立事件概率计算公式的合理运用.

| A. | -3 | B. | -2 | C. | -1 | D. | 3 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | -2 |
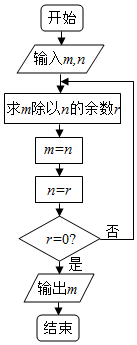 如图程序框图的算法思路源于古希腊数学家欧几里得的“辗转相除法”,执行该程序框图,若输入的m,n分别为153,119,则输出的m=( )
如图程序框图的算法思路源于古希腊数学家欧几里得的“辗转相除法”,执行该程序框图,若输入的m,n分别为153,119,则输出的m=( )