题目内容
15.函数y=3-2cos($\frac{2}{3}$x+$\frac{π}{3}$)的最大值为5,此时自变量x的取值集合是{x|x=3kπ+π,k∈Z}.分析 根据余弦函数的图象与性质,即可求出函数y=3-2cos($\frac{2}{3}$x+$\frac{π}{3}$)的最大值以及取最大值时x的取值集合.
解答 解:∵-1≤cos($\frac{2}{3}$x+$\frac{π}{3}$)≤1,
∴当cos($\frac{2}{3}$x+$\frac{π}{3}$)=-1时,
函数y=3-2cos($\frac{2}{3}$x+$\frac{π}{3}$)取得最大值5;
此时$\frac{2}{3}$x+$\frac{π}{3}$=2kπ+π,k∈Z,
解得x=3kπ+π,k∈Z;
故所求的x集合为{x|x=3kπ+π,k∈Z}.
故答案为:5,{x|x=3kπ+π,k∈Z}.
点评 本题考查了余弦函数的图象与性质的应用问题,是基础题目.

练习册系列答案
相关题目
20.命题p:x>y是命题q:x-3>y-4的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
14.已知函数f(x)=$\frac{1}{3}$x3+ax2+2x+2的图象在点(x0,f(x0))处的切线与直线x+y+1=0垂直,则实数a的取值范围为( )
| A. | [-1,1] | B. | (-1,1) | C. | (-∞,-1]∪[1,+∞) | D. | (-∞,-1)∪(1,+∞) |
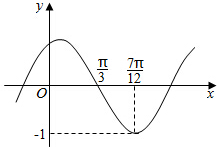 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示.