题目内容
求min{max{
,|x-6|}}.
| x |
考点:函数的最值及其几何意义
专题:计算题,函数的性质及应用
分析:由题意,先求
、|x-6|两个数中较大的数,从而得到max{
,|x-6|}=
,再求这个分段函数的最小值.
| x |
| x |
|
解答:
解:化简不等式
≥|x-6|可得,
x≥(x-6)2,
解得,4≤x≤9,
则max{
,|x-6|}=
,
则∵4≤x≤9,
∴2≤
≤3,
∵0≤x<4或x>9;
∴|x-6|>2,
故min{max{
,|x-6|}}=2.
| x |
x≥(x-6)2,
解得,4≤x≤9,
则max{
| x |
|
则∵4≤x≤9,
∴2≤
| x |
∵0≤x<4或x>9;
∴|x-6|>2,
故min{max{
| x |
点评:本题考查了分段函数的最值的求法,属于中档题.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
甲、乙两个同学分别解一道一元二次方程,甲因把一次项系数看错了,而解得方程两根为-3和5,乙把常数项看错了,解得两根为2+
和2-
,则原方程是( )
| 6 |
| 6 |
| A、x2+4x-15=0 |
| B、x2-4x+15=0 |
| C、x2+4x+15=0 |
| D、x2-4x-15=0 |
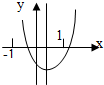 已知二次函数f(x)=ax2+bx+c(a≠0)的图象如图所示,设M=|a+b+c|-|a-b+c|+|2a+b|-|2a-b,则( )
已知二次函数f(x)=ax2+bx+c(a≠0)的图象如图所示,设M=|a+b+c|-|a-b+c|+|2a+b|-|2a-b,则( )| A、M>0 | B、M≥0 |
| C、M<0 | D、M=0 |
 如图,在三棱柱ABC-A1B1C1中,M为A1C1的中点,面AB1M∥面BC1N,CA∩面BC1N=N.求证:N为AC的中点.
如图,在三棱柱ABC-A1B1C1中,M为A1C1的中点,面AB1M∥面BC1N,CA∩面BC1N=N.求证:N为AC的中点.