题目内容
19.命题“?a∈R,a2≥0”的否定为( )| A. | ?a∈R,a2<0 | B. | ?a∈R,a2≥0 | C. | ?a∉R,a2≥0 | D. | ?a∈R,a2<0 |
分析 直接利用全称命题的否定是特称命题写出结果即可.
解答 解:因为全称命题的否定是特称命题,所以,命题“?a∈R,a2≥0”的否定为?a∈R,a2<0.
故选:D.
点评 本题考查命题的否定,特称命题与全称命题的否定关系,是基础题.

练习册系列答案
相关题目
10.如图所示的等腰直角三角形表示一个水平放置的平面图形的直观图,则这个平面图形的面积是( ) 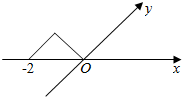

| A. | $2\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 1 | D. | $\frac{{\sqrt{2}}}{2}$ |
7.设数f(log2x)的定义域是(2,4),则函数$f({\frac{x}{2}})$的定义域是( )
| A. | (2,4) | B. | (2,8) | C. | (8,32) | D. | $(\frac{1}{2},1)$ |
4.在△ABC中,G为△ABC的重心,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,则$\overrightarrow{BG}$=( )
| A. | -$\frac{1}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$ | B. | $\frac{1}{3}$$\overrightarrow{a}$-$\frac{2}{3}$$\overrightarrow{b}$ | C. | -$\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$ | D. | $\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$ |
9.已知集合A={x|(x+1)(x-2)≤0},B={x|-2<x<2},则A∩B=( )
| A. | {x|-1≤x≤2} | B. | {x|-1≤x<2} | C. | {x|-1<x<2} | D. | {x|-2<x≤1} |
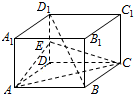 如图,正方体ABCD-A1B1C1D1的棱长为2,E为DD1的中点,
如图,正方体ABCD-A1B1C1D1的棱长为2,E为DD1的中点,