题目内容
某校高三年级一次数学考试之后,为了解学生的数学学习情况,随机抽取n名学生的数学成绩,制成如表所示的频率分布表.
(1)求a,b,n的值;
(2)若从第三,四,五组中用分层抽样方法抽取6名学生,并在这6名学生中随机抽取2名与张老师面谈,求第三组中至少有1名学生与张老师面谈的概率.
| 组号 | 分组 | 频数 | 频率 |
| 第一组 | [90,100) | 5 | 0.05 |
| 第二组 | [100,110) | a | 0.35 |
| 第三组 | [110,120) | 30 | 0.30 |
| 第四组 | [120,130) | 20 | b |
| 第五组 | [130,140) | 10 | 0.10 |
| 合 计 | n | 1.00 | |
(2)若从第三,四,五组中用分层抽样方法抽取6名学生,并在这6名学生中随机抽取2名与张老师面谈,求第三组中至少有1名学生与张老师面谈的概率.
考点:古典概型及其概率计算公式,分层抽样方法
专题:概率与统计
分析:(1)根据频率和频数的关系,依题意,得a,b,n的方程,解得即可,
(2)根据分层抽样,求出第三,四,五组抽取的学生的人数,然后一一列举取所有满足条件的基本事件,利用概率之和为1,求满足条件的概率.
(2)根据分层抽样,求出第三,四,五组抽取的学生的人数,然后一一列举取所有满足条件的基本事件,利用概率之和为1,求满足条件的概率.
解答:
解:(1)依题意,得
=0.05,
=0.35,
=b,
解得,n=100,a=35,b=0.2
(2)因为第三、四、五组共有60名学生,用分层抽样方法抽取6名学生,
则第三、四、五组分别抽取
×6=3名,
×6=2名,
×6=1名.
第三组的3名学生记为a1,a2,a3,第四组的2名学生记为b1,b2,第五组的1名学生记为c1,
则从6名学生中随机抽取2名,共有15种不同取法,具体如下:{a1,a2},{a1,a3},{a1,b1},{a1,b2},{a1,c1},{a2,a3},{a2,b1},
{a2,b2},{a2,c1},{a3,b1},{a3,b2},{a3,c1},{b1,b2},{b1,c1},{b2,c1}.
其中第三组的3名学生a1,a2,a3没有一名学生被抽取的情况共有3种,具体如下:{b1,b2},{b1,c1},{b2,c1}.
故第三组中至少有1名学生与张老师面谈的概率为1-
=0.8.
| 5 |
| n |
| a |
| n |
| 20 |
| n |
解得,n=100,a=35,b=0.2
(2)因为第三、四、五组共有60名学生,用分层抽样方法抽取6名学生,
则第三、四、五组分别抽取
| 30 |
| 60 |
| 20 |
| 60 |
| 10 |
| 60 |
第三组的3名学生记为a1,a2,a3,第四组的2名学生记为b1,b2,第五组的1名学生记为c1,
则从6名学生中随机抽取2名,共有15种不同取法,具体如下:{a1,a2},{a1,a3},{a1,b1},{a1,b2},{a1,c1},{a2,a3},{a2,b1},
{a2,b2},{a2,c1},{a3,b1},{a3,b2},{a3,c1},{b1,b2},{b1,c1},{b2,c1}.
其中第三组的3名学生a1,a2,a3没有一名学生被抽取的情况共有3种,具体如下:{b1,b2},{b1,c1},{b2,c1}.
故第三组中至少有1名学生与张老师面谈的概率为1-
| 3 |
| 15 |
点评:本题考查了频率与频数的关系以及分层抽样和古典概型的概率的求法,属于基础题.

练习册系列答案
相关题目
函数f(x)=cos2x+
sinxcosx在区间[-
,
]上的最大值为( )
| 3 |
| π |
| 4 |
| π |
| 3 |
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
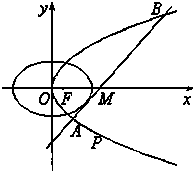 已知椭圆C1和抛物线C2有公共焦点F(1,0),C1的中心和C2的顶点都在坐标原点,过点M(4,0)的直线l与抛物线C2分别相交于A,B两点.
已知椭圆C1和抛物线C2有公共焦点F(1,0),C1的中心和C2的顶点都在坐标原点,过点M(4,0)的直线l与抛物线C2分别相交于A,B两点. 如图,⊙O为四边形ABCD的外接圆,且AB=AD,E是CB延长线上一点,直线EA与圆O相切.求证:
如图,⊙O为四边形ABCD的外接圆,且AB=AD,E是CB延长线上一点,直线EA与圆O相切.求证: