题目内容
已知|
|=1,|
|=
,且
•(2
+
)=1,则
与
夹角的余弦值为( )
| a |
| b |
| 2 |
| b |
| a |
| b |
| a |
| b |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
考点:平面向量数量积的运算
专题:平面向量及应用
分析:设
与
夹角为θ,由题意可得 2
•
+
2=1,再利用两个向量的数量积的定义,求得cosθ的值.
| a |
| b |
| a |
| b |
| b |
解答:
解:设
与
夹角为θ,由题意可得 2
•
+
2=1,即 2×1×
×cosθ+2=1,
∴cosθ=-
,
故选:B.
| a |
| b |
| a |
| b |
| b |
| 2 |
∴cosθ=-
| ||
| 4 |
故选:B.
点评:本题主要考查两个向量的数量积的定义,属于基础题.

练习册系列答案
相关题目
一条直线与两条异面直线中的一条相交,那么它与另一条直线之间的位置关系是( )
| A、异面 | B、相交或平行或异面 |
| C、相交 | D、平行 |
设f(x)=
,则f[f(ln2+1)]=( )
|
| A、log717 |
| B、2 |
| C、7 |
| D、log7(8e2+1) |
若直线l:y=-
+m与曲线C:y=
有且仅有三个交点,则m的取值范围是( )
| x |
| 2 |
| 1 |
| 2 |
| |4-x2| |
A、(
| ||||
B、(1,
| ||||
C、(1,
| ||||
D、(2,
|
一个样本a,3,5,7的平均数是5,则这个样本的方差是( )
| A、2 | ||
B、
| ||
| C、4 | ||
| D、1 |
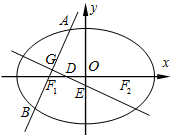 如图,已知椭圆C:
如图,已知椭圆C: