题目内容
11.已知f(x)=log2(1+x)-log2(1-x)(1)求f(x)的定义域;
(2)判断f(x)的奇偶性并加以说明;
(3)求使f(x)>0的x的取值范围.
分析 (1)由对数式有意义可得1+x>0且1-x>0,解不等式可得定义域;
(2)由奇偶性的定义可得函数为奇函数;
(3)f(x)>0可化为1+x>1-x>0,即可求使f(x)>0的x的取值范围.
解答 解:(1)由对数式有意义可得1+x>0且1-x>0,
解得-1<x<1,∴函数f(x)的定义域为(-1,1),
(2)∵f(-x)=log2(1-x)-log2(1+x)=-f(x),
∴结合定义域关于原点对称可得f(x)为奇函数;
(3)f(x)=log2(1+x)-log2(1-x)>0
可得1+x>1-x>0,
∴0<x<1.
点评 本题考查对数函数的图象和性质,涉及对数不等式的解法,属基础题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
2.关于幂函数y=xk及其图象,有下列四个命题:
①其图象一定不通过第四象限;
②当k<0时,其图象关于直线y=x对称;
③当k>0时,函数y=xk是增函数;
④y=xk的图象与y=x-k的图象至少有两个交点
其中正确的命题个数是( )
①其图象一定不通过第四象限;
②当k<0时,其图象关于直线y=x对称;
③当k>0时,函数y=xk是增函数;
④y=xk的图象与y=x-k的图象至少有两个交点
其中正确的命题个数是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
19.向量a=(2,-2),b=(4,x)且a,b共线,则x的值为( )
| A. | 1 | B. | -1 | C. | -3 | D. | -4 |
16.函数$f(x)=({1-\frac{2}{{1+{2^x}}}})tanx$的图象( )
| A. | 关于x轴对称 | B. | 关于y轴对称 | C. | 关于y=x轴对称 | D. | 关于原点轴对称 |
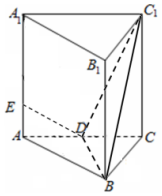 已知正三棱柱ABC-A1B1C1中,AB=AA1=2,点D为AC的中点,点E为AA1上.
已知正三棱柱ABC-A1B1C1中,AB=AA1=2,点D为AC的中点,点E为AA1上.
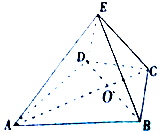 如图,在四棱锥E-ABCD中,△ABD是正三角形,△BCD是等腰三角形,∠BCD=120°,EC⊥BD.
如图,在四棱锥E-ABCD中,△ABD是正三角形,△BCD是等腰三角形,∠BCD=120°,EC⊥BD.