题目内容
20.某市为了制定合理的节电方案,供电局对居民用电进行了调查,通过抽样,获得了某年200户居民每户的月均用电量(单位:度),将数据按照[0,100),[100,200),[200,300),[300,400),[400,500),[500,600),[600,700),[700,800),[800,900]分成9组,制成了如图所示的频率分布直方图.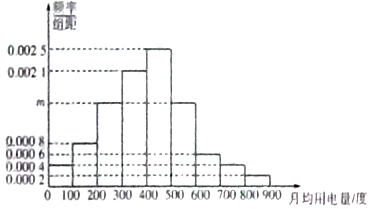
(Ⅰ)求直方图中m的值并估计居民月均用电量的中位数;
(Ⅱ)现从第8组和第9组的居民中任选取2户居民进行访问,则两组中各有一户被选中的概率.
分析 (Ⅰ)根据频率分布直方图求出m的值;(Ⅱ)根据条件概率求出两组中各有一户被选中的概率即可.
解答 解:(Ⅰ)1-100×(0.0004+0.0008+0.0021+0.0025+0.0006+0.0004+0.0002)=2m×100,
∴m=0.0015.
设中位数是x度,前5组的频率之和为0.04+0.08+0.15+0.21+0.25=0.73>0.5,
而前4组的频率之和为0.04+0.08+0.15+0.21=0.48<0.5,
所以400<x<500,$x-400=\frac{0.5-0.48}{0.25}×100$,
故x=408,即居民月均用电量的中位数为408度.
(Ⅱ)第8组的户数为0.0004×100×100=4,分别设为A1,A2,A3,A4,
第9组的户数为0.0002×100×100=2,分别设为B1,B2,
则从中任选出2户的基本事件为:
(A1,A2),(A1,A3),(A1,A4),(A1,B1),(A1,B2),
(A2,A3),(A2,A4),(A2,B1),(A2,B2),(A3,A4),
(A3,B1),(A3,B2),(A4,B1),(A4,B2),(B1,B2)共15种.
其中两组中各有一户被选中的基本事件为:
(A1,B1),(A1,B2),(A2,B1),(A2,B2),
(A3,B1),(A3,B2),(A4,B1),(A4,B2)共8种.
所以第8,9组各有一户被选中的概率$P=\frac{8}{15}$.
点评 本题考查了频率分布直方图问题,考查条件概率问题,是一道中档题.

练习册系列答案
相关题目
15.某民调机构为了了解民众是否支持英国脱离欧盟,随机抽调了100名民众,他们的年龄的频数及支持英国脱离欧盟的人数分布如下表:
(Ⅰ)由以上统计数据填下面列联表,并判断是否有99%的把握认为以50岁胃分界点对是否支持脱离欧盟的态度有差异;
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
(Ⅱ)若采用分层抽样的方式从18-64岁且支持英国脱离欧盟的民众中选出7人,再从这7人中随机选出2人,求这2人至少有1人年龄在18-24岁的概率.
| 年龄段 | 18-24岁 | 25-49岁 | 50-64岁 | 65岁及以上 |
| 频数 | 35 | 20 | 25 | 20 |
| 支持脱欧的人数 | 10 | 10 | 15 | 15 |
| 年龄低于50岁的人数 | 年龄不低于50岁的人数 | 合计 | |
| 支持“脱欧”人数 | |||
| 不支持“脱欧”人数 | |||
| 合计 |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| K0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
5.直线${l_1}:x+{a^2}y+6=0$和直线l2:(a-2)x+3ay+2a=0.若l1∥l2,则a的值为( )
| A. | -1 | B. | 0 | C. | 0或-1 | D. | 0或1 |
12.如图所示的程序框图中,输出的B是( )
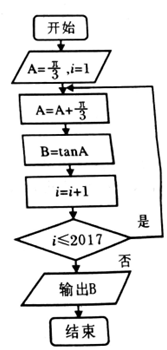

| A. | $\sqrt{3}$ | B. | 0 | C. | -$\frac{\sqrt{3}}{3}$ | D. | -$\sqrt{3}$ |