题目内容
已知k∈R且k≠1,直线l1:y=
x+1和l2:y=
x-k.
(1)求直线l1∥l2的充要条件;
(2)当x∈[-1,2]时,直线l1恒在x轴上方,求k的取值范围.
| k |
| 2 |
| 1 |
| k-1 |
(1)求直线l1∥l2的充要条件;
(2)当x∈[-1,2]时,直线l1恒在x轴上方,求k的取值范围.
考点:直线的斜率
专题:直线与圆
分析:(1)利用斜率存在的两条直线平行的充要条件
解得即可.
(2)法1:利用直线的单调性即可得出;
法2:通过对斜率分类讨论,再利用单调性即可得出.
|
(2)法1:利用直线的单调性即可得出;
法2:通过对斜率分类讨论,再利用单调性即可得出.
解答:
解:(1)由题意得
解得k=2.
当k=2时,l1:y=x+1,l2:y=x-2,
此时l1∥l2.
(2)设f(x)=
x+1.
法1:由题意得
,即
,解得-1<k<2.
法2:
或
,解得-1<k<2.
|
当k=2时,l1:y=x+1,l2:y=x-2,
此时l1∥l2.
(2)设f(x)=
| k |
| 2 |
法1:由题意得
|
|
法2:
|
|
点评:本题考查了斜率存在的两条直线平行的充要条件、直线的单调性、分类讨论方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
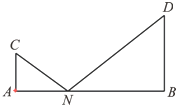 如图,C,D是两个小区的所在地,C,D到一条公路AB的垂直距离CA=1km,DB=2km,AB两端之间的距离为4km.某公交公司将在AB之间找一点N,在N处建造一个公交站台.
如图,C,D是两个小区的所在地,C,D到一条公路AB的垂直距离CA=1km,DB=2km,AB两端之间的距离为4km.某公交公司将在AB之间找一点N,在N处建造一个公交站台.