题目内容
8.定义域为[-1,1]上的奇函数f(x)满足f(x)=f(x-2),且当x∈(0,1)时,f(x)=$\frac{a^x}{a^{2x}+1}$(a>1).(1)求f(1)的值;
(2)求函数f(x)的解析式;
(3)求函数f(x)的值域.
分析 (1)利用函数奇偶性的关系令x=1,即可求f(1)的值;
(2)根据函数奇偶性的性质利用对称性即可求函数f(x)的解析式;
(3)根据函数单调性的性质判断函数的单调性即可求函数f(x)的值域.
解答 解:(1)∵定义域为[-1,1]上的奇函数f(x)满足f(x)=f(x-2),
∴f(1)=f(1-2)=f(-1)=-f(1),
∴f(1)=0…(3分)
(2)当x∈(-1,0)时,-x∈(0,1),
则f(x)=-f(-x)=-$\frac{{a}^{-x}}{{a}^{-2x}+1}$=-$\frac{a^x}{a^{2x}+1}$,…(5分)
又∵f(x)为[-1,1]上的奇函数,
∴f(0)=0,
即f(x)=$\left\{\begin{array}{l}{\frac{{a}^{x}}{{a}^{2x}+1},}&{x∈(0,1)}\\{0,}&{x=1或±1}\\{-\frac{{a}^{x}}{{a}^{2x}+1},}&{x∈(-1,0)}\end{array}\right.$…(7分)
(3)∵当x∈(0,1)时,ax∈(1,a)…(8分),
设t=ax,y=t+$\frac{1}{t}$,1<t<a,
任取1<t1<a,1<t2<a,且t1<t2,
则y(t2)-y(t1)=t2+$\frac{1}{{t}_{2}}$-(t1+$\frac{1}{{t}_{1}}$)=(t2-t1)+($\frac{1}{{t}_{2}}$-$\frac{1}{{t}_{1}}$)=(t2-t1)•$\frac{{t}_{1}{t}_{2}-1}{{t}_{1}{t}_{2}}$,
∵1<t1<a,1<t2<a,且t1<t2,
∴t2-t1>0,t2t1>1,
则y(t2)-y(t1)=(t2-t1)•$\frac{{t}_{1}{t}_{2}-1}{{t}_{1}{t}_{2}}$>0,
即y(t2)>y(t1),
即函数y=t+$\frac{1}{t}$,在1<t<a上为增函数,
∴ax+$\frac{1}{{a}^{x}}$∈(2,$\frac{{a}^{2}+1}{a}$),
∴$\frac{a^x}{a^{2x}+1}$=$\frac{1}{{a}^{x}+\frac{1}{{a}^{x}}}$∈($\frac{a}{{a}^{2}+1}$,$\frac{1}{2}$).
∴函数f(x)的值域为(-$\frac{1}{2}$,-$\frac{a}{{a}^{2}+1}$)∪{0}∪($\frac{a}{{a}^{2}+1}$,$\frac{1}{2}$).(12分)
点评 本题主要考查函数值以及函数解析式的求解以及函数值域的计算,利用函数奇偶性和单调性的性质是解决本题的关键.

 名校通行证有效作业系列答案
名校通行证有效作业系列答案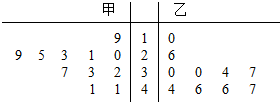 某苗圃基地为了解基地内甲、乙两块地种植同一种树苗的长势情况,从两块地各随机抽取了10株树苗,用茎叶图表示上述两组树苗高度的数据,对两块地抽取树苗的高度的平均数$\overline{x}$甲,$\overrightarrow{x}$乙和方差进行比较,下面结论正确的是( )
某苗圃基地为了解基地内甲、乙两块地种植同一种树苗的长势情况,从两块地各随机抽取了10株树苗,用茎叶图表示上述两组树苗高度的数据,对两块地抽取树苗的高度的平均数$\overline{x}$甲,$\overrightarrow{x}$乙和方差进行比较,下面结论正确的是( )| A. | $\overline{x}$甲>$\overrightarrow{x}$乙,乙地树苗高度比甲地树苗高度更稳定 | |
| B. | $\overline{x}$甲<$\overrightarrow{x}$乙,甲地树苗高度比乙地树苗高度更稳定 | |
| C. | $\overline{x}$甲<$\overrightarrow{x}$乙,乙地树苗高度比甲地树苗高度更稳定 | |
| D. | $\overline{x}$甲>$\overrightarrow{x}$乙,甲地树苗高度比乙地树苗高度更稳定 |
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
| A. | (-∞,3] | B. | (-∞,-3) | C. | [2,3) | D. | [-3,2) |