题目内容
20.如图,在圆C中,是不是只需知道圆C的半径或弦AB的长度,就可以求$\overrightarrow{AB}$•$\overrightarrow{AC}$的值?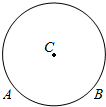
分析 由题意设$\overrightarrow{AB}$与$\overrightarrow{AC}$的夹角为θ,取AB中点M,连结CM,则CM⊥AB,根据向量的数量积公式即可求出.
解答 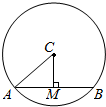 解:设$\overrightarrow{AB}$与$\overrightarrow{AC}$的夹角为θ,取AB中点M,连结CM,则CM⊥AB,
解:设$\overrightarrow{AB}$与$\overrightarrow{AC}$的夹角为θ,取AB中点M,连结CM,则CM⊥AB,
∴cosθ=$\frac{|\overrightarrow{AM}|}{|\overrightarrow{AC}|}$=$\frac{\frac{1}{2}|\overrightarrow{AB}|}{|\overrightarrow{AC}|}$,
∴$\overrightarrow{AB}$•$\overrightarrow{AC}$=|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|cosθ=|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|$\frac{\frac{1}{2}|\overrightarrow{AB}|}{|\overrightarrow{AC}|}$=$\frac{1}{2}$|$\overrightarrow{AB}$|2,
∴$\overrightarrow{AB}$与$\overrightarrow{AC}$的值只与弦AB的长度有关,与半径无关.
点评 本题主要考查了向量的运算,以及三角函数中,角与边的关系,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.甲、乙两艘救助船相距1海里,经测量求救呼叫信号发出的位置与这两船构成的角度是救助船甲与救助船乙、求救呼叫信号发出的位置所构成角度的一半,可以判断三者构成的三角形是锐角三角形,则求救呼叫信号发出的位置与救助船乙的距离范围是( )
| A. | (1,2) | B. | (1,$\sqrt{2}$) | C. | (1,$\sqrt{3}$) | D. | ($\sqrt{2}$,$\sqrt{3}$) |
10.若直线(3a+2)x-3y+8=0和直线3x+(a+4)y-7=0相互垂直,则a的值为( )
| A. | 0 | B. | 1 | C. | 0或1 | D. | 0或-1 |
 已知函数f(x)=sin(ωx+φ)($ω>0,|φ|<\frac{π}{2}$)的部分图象如图所示,那么ω=2,φ=$\frac{π}{6}$.
已知函数f(x)=sin(ωx+φ)($ω>0,|φ|<\frac{π}{2}$)的部分图象如图所示,那么ω=2,φ=$\frac{π}{6}$.