题目内容
15.若a,b,c∈R,且a>b,则下列不等式一定成立的是( )| A. | a+c>b-c | B. | ac>bc | C. | a2>b2 | D. | (a-b)c2≥0 |
分析 利用不等式的基本性质,直接写出结果即可.
解答 解:a,b,c∈R,且a>b,可得a-b>0,
c2≥0,
可得(a-b)c2≥0.
故选:D.
点评 本题考查不等式的简单性质的应用,是基础题.

练习册系列答案
相关题目
6.某校高一年级有四个班,其中一、二班为数学课改班,三、四班为数学非课改班.在期末考试中,课改班与非课改班的数学成绩优秀与非优秀人数统计如下表.
(Ⅰ)求d的值为多少?若采用分层抽样的方法从课改班的学生中随机抽取4人,则数学成绩优秀和数学成绩非优秀抽取的人数分别是多少?
(Ⅱ)在(Ⅰ)的条件下抽取的4人中,再从中随机抽取2人,求两人数学成绩都优秀的概率.
| 优秀 | 非优秀 | 总计 | |
| 课改班 | a | 50 | b |
| 非课改班 | 20 | c | 110 |
| 合计 | d | e | 210 |
(Ⅱ)在(Ⅰ)的条件下抽取的4人中,再从中随机抽取2人,求两人数学成绩都优秀的概率.
5.已知P1(2,-1),P2(0,5),点P在P1P2的延长线上,且|$\overrightarrow{{P}_{1}P}$|=3|$\overrightarrow{P{P}_{2}}$|,则点P的坐标为( )
| A. | (1,2) | B. | ($\frac{4}{3}$,3) | C. | ($\frac{2}{3}$,3) | D. | (-1,8) |
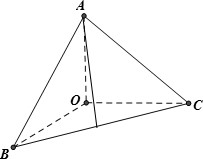 如图所示,在三棱锥A-OBC中,OA,OB,OC两两垂直且长度都为2,则这个三棱锥的体积为$\frac{4}{3}$;O到平面ABC的距离为$\frac{2\sqrt{3}}{3}$.
如图所示,在三棱锥A-OBC中,OA,OB,OC两两垂直且长度都为2,则这个三棱锥的体积为$\frac{4}{3}$;O到平面ABC的距离为$\frac{2\sqrt{3}}{3}$.