题目内容
15.设$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°,且|$\overrightarrow{a}$|=2$\sqrt{2}$,|$\overrightarrow{b}$|=$\sqrt{3}$,则$\overrightarrow{a}$•$\overrightarrow{b}$=$\sqrt{6}$.分析 根据向量数量积的定义计算.
解答 解:$\overrightarrow{a}•\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos60°$=2$\sqrt{2}×\sqrt{3}×\frac{1}{2}$=$\sqrt{6}$.
故答案为:$\sqrt{6}$.
点评 本题考查了平面向量的数量积运算,属于基础题.

练习册系列答案
相关题目
20.一个长方体底面为正方形且边长为4,高为h,若这个长方体能装下8个半径为1的小球和一个半径为2的大球,则h的最小值为( )
| A. | 8 | B. | 2+2$\sqrt{7}$ | C. | 2+2$\sqrt{5}$ | D. | 6 |
7.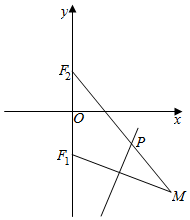 如图所示,点F1(0,-$\sqrt{2}$),F2(0,$\sqrt{2}$),动点M到点F2的距离是4,线段MF1的中垂线交MF2于点P.当点M变化时,则动点P的轨迹方程为( )
如图所示,点F1(0,-$\sqrt{2}$),F2(0,$\sqrt{2}$),动点M到点F2的距离是4,线段MF1的中垂线交MF2于点P.当点M变化时,则动点P的轨迹方程为( )
 如图所示,点F1(0,-$\sqrt{2}$),F2(0,$\sqrt{2}$),动点M到点F2的距离是4,线段MF1的中垂线交MF2于点P.当点M变化时,则动点P的轨迹方程为( )
如图所示,点F1(0,-$\sqrt{2}$),F2(0,$\sqrt{2}$),动点M到点F2的距离是4,线段MF1的中垂线交MF2于点P.当点M变化时,则动点P的轨迹方程为( )| A. | $\frac{x^2}{4}+\frac{y^2}{2}=1$ | B. | $\frac{{y}^{2}}{4}$+$\frac{{x}^{2}}{2}$=1 | C. | x2+y2=1 | D. | $\frac{y^2}{4}-\frac{x^2}{2}=1$ |
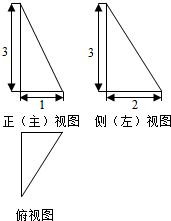
4.一个几何体的三视图如所示,则该几何体的体积是( )


| A. | $\frac{2}{3}$π+4 | B. | 2π+4 | C. | π+4 | D. | π+2 |
5.若集合A=[2,3],B={x|x2-5x+6=0|,则A∩B=( )
| A. | {2,3} | B. | ∅ | C. | 2 | D. | [2,3] |