题目内容
7.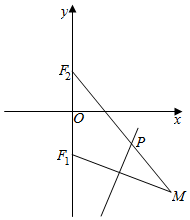 如图所示,点F1(0,-$\sqrt{2}$),F2(0,$\sqrt{2}$),动点M到点F2的距离是4,线段MF1的中垂线交MF2于点P.当点M变化时,则动点P的轨迹方程为( )
如图所示,点F1(0,-$\sqrt{2}$),F2(0,$\sqrt{2}$),动点M到点F2的距离是4,线段MF1的中垂线交MF2于点P.当点M变化时,则动点P的轨迹方程为( )| A. | $\frac{x^2}{4}+\frac{y^2}{2}=1$ | B. | $\frac{{y}^{2}}{4}$+$\frac{{x}^{2}}{2}$=1 | C. | x2+y2=1 | D. | $\frac{y^2}{4}-\frac{x^2}{2}=1$ |
分析 由图形结合椭圆定义可得动点P的轨迹方程.
解答  解:如图,连接PF1,
解:如图,连接PF1,
∵P是线段MF1 的垂直平分线上的点,
∴|PM|=|PF1|,则|PF1|+|PF2|=|MF2|=4$>2\sqrt{2}$,
∴当点M变化时,则动点P的轨迹是以F1、F2为焦点的椭圆,
此时2a=4,a=2,c=$\sqrt{2}$,则b2=a2-c2=2.
∴动点P的轨迹方程为$\frac{{y}^{2}}{4}+\frac{{x}^{2}}{2}=1$.
故选:B.
点评 本题考查椭圆的简单性质,考查了椭圆标准方程的求法,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知函数f(x)为奇函数,当x≥0时,f(x)=log2(x+l)+m,则f(1-$\sqrt{2}$)的值为( )
| A. | -$\frac{1}{2}$ | B. | -log2(2-$\sqrt{2}$) | C. | $\frac{1}{2}$ | D. | log2(2-$\sqrt{2}$) |
 已知椭圆C的中心在原点,离心率等于$\frac{1}{2}$,它的一个短轴端点点恰好是抛物线$y=\frac{{\sqrt{3}}}{24}{x^2}$的焦点.
已知椭圆C的中心在原点,离心率等于$\frac{1}{2}$,它的一个短轴端点点恰好是抛物线$y=\frac{{\sqrt{3}}}{24}{x^2}$的焦点.