题目内容
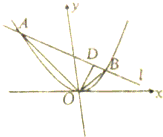 如图,已知直线l与顶点在原点O,焦点在y轴的正半轴上的抛物线C相交于A,B两点,且OA⊥OB,垂足D的坐标为(1,2).
如图,已知直线l与顶点在原点O,焦点在y轴的正半轴上的抛物线C相交于A,B两点,且OA⊥OB,垂足D的坐标为(1,2).(1)求直线l的方程;
(2)求抛物线C的方程.
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(1)由题意OD⊥AB且D的坐标为(1,2),求出OD的斜率,由两条直线垂直的条件求出直线l的斜率,代入点斜式方程再化为一般式方程;
(2)由题意设抛物线的方程是x2=2py(p>0)和点A、B的坐标,联立直线l的方程消去y,利用韦达定理求出x1+x2和x1x2,由OA⊥OB得
•
=0,利用向量的数量积运算化简,列出关于p的方程求解即可.
(2)由题意设抛物线的方程是x2=2py(p>0)和点A、B的坐标,联立直线l的方程消去y,利用韦达定理求出x1+x2和x1x2,由OA⊥OB得
| OA |
| OB |
解答:
解:(1)由题意得,OD⊥AB,且D的坐标为(1,2),
则OD的斜率是2,所以直线l的斜率是-
,
所以直线l的方程是y-2=-
(x-1),即x+2y-5=0;
(2)设抛物线的方程是x2=2py(p>0),且A(x1,y1),B(x2,y2),
由
得,x2+px-5p=0,
则△=p2+20p>0,且x1+x2=-p,x1x2=-5p,
因为OA⊥OB,所以
•
=0,
则x1x2+y1y2=0,即x1x2+
=0,
所以-5p+
=0,解得p=
,
所以抛物线的方程是x2=
y.
则OD的斜率是2,所以直线l的斜率是-
| 1 |
| 2 |
所以直线l的方程是y-2=-
| 1 |
| 2 |
(2)设抛物线的方程是x2=2py(p>0),且A(x1,y1),B(x2,y2),
由
|
则△=p2+20p>0,且x1+x2=-p,x1x2=-5p,
因为OA⊥OB,所以
| OA |
| OB |
则x1x2+y1y2=0,即x1x2+
| x12x22 |
| 4p2 |
所以-5p+
| 25p2 |
| 4p2 |
| 5 |
| 4 |
所以抛物线的方程是x2=
| 5 |
| 2 |
点评:本题考查直线、抛物线的方程,垂直问题转化为两条直线垂直的条件、向量的数量积问题,以及韦达定理的应用,直线与圆锥曲线的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若A={1,3,-1},B={0,1},则A∪B=( )
| A、{1} |
| B、{0,1,3,-1} |
| C、{0,3,-1} |
| D、{0,1,3} |
已知点A在曲线P:y=x2(x>0)上,⊙A过原点O,且与y轴的另一个交点为M.若线段OM,⊙A和曲线P上分别存在点B、点C和点D,使得四边形ABCD(点A,B,C,D顺时针排列)是正方形,则称点A为曲线P的“完美点”.那么下列结论中正确的是( )
| A、曲线P上不存在“完美点” | ||
| B、曲线P上只存在一个“完美点”,其横坐标大于1 | ||
C、曲线P上只存在一个“完美点”,其横坐标大于
| ||
D、曲线P上存在两个“完美点”,其横坐标均大于
|
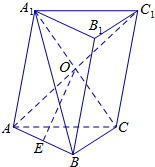 如图,斜三棱柱ABC-A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,E是AB的中点.求证:
如图,斜三棱柱ABC-A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,E是AB的中点.求证: