题目内容
已知在直三棱柱ABC-A1B1C1中,AB=1,BC=2,AC=
,AA1=3,M为线段BB1上的一动点,则当AM+MC1最小时,△AMC1的面积为 .
| 15 |
考点:棱柱的结构特征
专题:空间位置关系与距离
分析:先将直三棱柱ABC-A1B1C1沿棱BB1展开成平面连接AC1,与BB1的交点即为满足AM+MC1最小时的点M,由此可以求得△AMC1的三边长,再由余弦定理求出其中一角,由面积公式求出面积.
解答:
 解:将直三棱柱ABC-A1B1C1沿棱BB1展开成平面连接AC1,与BB1的交点即为满足AM+MC1最小时的点M,
解:将直三棱柱ABC-A1B1C1沿棱BB1展开成平面连接AC1,与BB1的交点即为满足AM+MC1最小时的点M,
由于AB=1,BC=2,AA1=3,再结合棱柱的性质,可得BM=
AA1=1,故B1M=2,
∴AM=
,AC1=2
,MC1=2
,
cos∠AMC1=
=
=-
,
∴sin∠AMC1=
,
∴△AMC1的面积
×
×2
×
=1.
故答案为1.
 解:将直三棱柱ABC-A1B1C1沿棱BB1展开成平面连接AC1,与BB1的交点即为满足AM+MC1最小时的点M,
解:将直三棱柱ABC-A1B1C1沿棱BB1展开成平面连接AC1,与BB1的交点即为满足AM+MC1最小时的点M,由于AB=1,BC=2,AA1=3,再结合棱柱的性质,可得BM=
| 1 |
| 3 |
∴AM=
| 2 |
| 6 |
| 2 |
cos∠AMC1=
| AM2+MC12-AC12 |
| 2AM•MC1 |
=
| 2+8-24 | ||
8
|
| ||
| 2 |
∴sin∠AMC1=
| 1 |
| 2 |
∴△AMC1的面积
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
故答案为1.
点评:本题重点考查了棱柱的结构特征、侧面展开图等知识,属于中档题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
“1<m<2”是“方程
+
=1表示的曲线是焦点在y轴上的椭圆”的( )
| x2 |
| m-1 |
| y2 |
| 3-m |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知全集U={0,1,2},且∁UA={2},则集合A等于( )
| A、{0} | B、{0,1} |
| C、{1} | D、∅ |
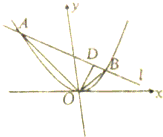 如图,已知直线l与顶点在原点O,焦点在y轴的正半轴上的抛物线C相交于A,B两点,且OA⊥OB,垂足D的坐标为(1,2).
如图,已知直线l与顶点在原点O,焦点在y轴的正半轴上的抛物线C相交于A,B两点,且OA⊥OB,垂足D的坐标为(1,2).