题目内容
已知点A在曲线P:y=x2(x>0)上,⊙A过原点O,且与y轴的另一个交点为M.若线段OM,⊙A和曲线P上分别存在点B、点C和点D,使得四边形ABCD(点A,B,C,D顺时针排列)是正方形,则称点A为曲线P的“完美点”.那么下列结论中正确的是( )
| A、曲线P上不存在“完美点” | ||
| B、曲线P上只存在一个“完美点”,其横坐标大于1 | ||
C、曲线P上只存在一个“完美点”,其横坐标大于
| ||
D、曲线P上存在两个“完美点”,其横坐标均大于
|
考点:二次函数的性质
专题:新定义
分析:假设点A为“完美点”,画出图象,设A(m,m2),通过讨论m<1时,m≥1时的情况从而得到答案.
解答:
解:如下图左,如果点A为“完美点”,则AB=AD=
AC=
OA,
以A为圆心,
OA为半径作圆T(如下图右中虚线圆),
交y轴于点B,B′(可重合),交抛物线于点D,D′,
点A为“完美点”当且仅当AB⊥AD,若下图右,
(结合图象知,B点一定是上方的交点,否则在抛物线上不存在D点使得AB⊥AD;
D也一定是上方的交点,否则A,B,C,D不是顺时针),
 ,
, ,
,
下面考虑当点A的横坐标越来越大时∠BAD的变化情况,
设A(m,m2),当m<1时,∠AOY=45°,
此时圆T与y轴相离或相切时,此时A不是完美点,
故只需考虑m≥1,当m增加时,∠BAD越来越小,且趋近于0,(推理在后面),
而当m=1时,∠BAD>90°,
故曲线P上存在唯一一个完美点,其横坐标大于1,
当m增加时,∠BAD越来越小,且趋近于0°的推理:
过A作AH⊥y轴于点H,
分别过点A,D作x轴,y轴的平行线交于N,
先考虑∠BAH:cos∠BAH=
=
,
于是m增大时,cos∠BAH减小且趋于0,从而∠BAH增大,且趋于90°,
再考虑∠DAN,记D(n,n2),则tan∠DAN=
=n+m,
随着m的增大,OA的长增大,AD=
OA也增大,
于是m+n增大,从而tan∠DAN增大,∠DAN增大且趋近于90°,
∴∠BAD=π-∠BAH-∠DAN随着m的增大而减小,且趋于0°,
故选:B.
| ||
| 2 |
| ||
| 2 |
以A为圆心,
| ||
| 2 |
交y轴于点B,B′(可重合),交抛物线于点D,D′,
点A为“完美点”当且仅当AB⊥AD,若下图右,
(结合图象知,B点一定是上方的交点,否则在抛物线上不存在D点使得AB⊥AD;
D也一定是上方的交点,否则A,B,C,D不是顺时针),
 ,
, ,
,下面考虑当点A的横坐标越来越大时∠BAD的变化情况,
设A(m,m2),当m<1时,∠AOY=45°,
此时圆T与y轴相离或相切时,此时A不是完美点,
故只需考虑m≥1,当m增加时,∠BAD越来越小,且趋近于0,(推理在后面),
而当m=1时,∠BAD>90°,
故曲线P上存在唯一一个完美点,其横坐标大于1,
当m增加时,∠BAD越来越小,且趋近于0°的推理:
过A作AH⊥y轴于点H,
分别过点A,D作x轴,y轴的平行线交于N,
先考虑∠BAH:cos∠BAH=
| m | ||||||
|
| ||
|
于是m增大时,cos∠BAH减小且趋于0,从而∠BAH增大,且趋于90°,
再考虑∠DAN,记D(n,n2),则tan∠DAN=
| n2-m2 |
| n-m |
随着m的增大,OA的长增大,AD=
| ||
| 2 |
于是m+n增大,从而tan∠DAN增大,∠DAN增大且趋近于90°,
∴∠BAD=π-∠BAH-∠DAN随着m的增大而减小,且趋于0°,
故选:B.
点评:本题考查了新定义问题,考查了二次函数的性质,考查了数形结合思想,本题有一定难度.

练习册系列答案
相关题目
已知变量x、y满足约束条件
,则目标函数z=3x-y的最大值是( )
|
| A、6 | ||
| B、-1 | ||
| C、1 | ||
D、
|
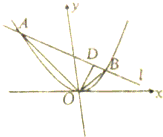 如图,已知直线l与顶点在原点O,焦点在y轴的正半轴上的抛物线C相交于A,B两点,且OA⊥OB,垂足D的坐标为(1,2).
如图,已知直线l与顶点在原点O,焦点在y轴的正半轴上的抛物线C相交于A,B两点,且OA⊥OB,垂足D的坐标为(1,2).
