题目内容
已知函数f(x)=ax2+(b-
)x+c(a≠0)过坐标原点,且在x=1处的切线方程为x-y-1=0.
(1)求f(x)的解析式;
(2)设g(x)=lnx-f(x)f′(x),求g(x)的最大值及相应的x值;
(3)对于任意正数x,恒有f(x)+f(
)-2≥(x+
)•lnm,求实数m的取值范围.
| 1 |
| 2 |
(1)求f(x)的解析式;
(2)设g(x)=lnx-f(x)f′(x),求g(x)的最大值及相应的x值;
(3)对于任意正数x,恒有f(x)+f(
| 1 |
| x |
| 1 |
| x |
考点:利用导数研究曲线上某点切线方程,二次函数的性质
专题:计算题,函数的性质及应用,导数的综合应用
分析:(1)由函数f(x)=ax2+(b-
)x+c(a≠0)过坐标原点可得f(0)=c=0,从而求导f′(x)=2ax+(b-
),从而得到f′(1)=2a+(b-
)=1且f(1)=a+b-
=0;从而解得;
(2)化简g(x)=lnx-f(x)f′(x)=lnx-2x3+3x2-x;求导g′(x)=
;从而求最值;
(3)x>0时,不等式x2+
-(x+
)-2≥(x+
)•lnm恒成立,令x+
=t,(t≥2),则lnm≤t-
-1;从而求得.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)化简g(x)=lnx-f(x)f′(x)=lnx-2x3+3x2-x;求导g′(x)=
| (x-1)(6x2+1) |
| x |
(3)x>0时,不等式x2+
| 1 |
| x2 |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 4 |
| t |
解答:
解:(1)∵函数f(x)=ax2+(b-
)x+c(a≠0)过坐标原点,
∴f(0)=c=0,
∴f′(x)=2ax+(b-
),
由函数f(x)在x=1处的切线方程为x-y-1=0知,
f′(1)=2a+(b-
)=1且f(1)=a+b-
=0;
解得a=1,b=-
;
∴f(x)=x2-x.
(2)g(x)=lnx-f(x)f′(x)=lnx-2x3+3x2-x;
∵g′(x)=
;
∴当x∈(0,1)时,g(x)单调递增;当x∈(1,+∞)时,g(x)单调递减.
∴当x=1时,g(x)有最大值,且gmax(x)=0;
(3)x>0时,不等式x2+
-(x+
)-2≥(x+
)•lnm恒成立,
令x+
=t,(t≥2),则lnm≤t-
-1;
∴lnm≤(t-
-1)min=-1;
∴0<m≤
.
| 1 |
| 2 |
∴f(0)=c=0,
∴f′(x)=2ax+(b-
| 1 |
| 2 |
由函数f(x)在x=1处的切线方程为x-y-1=0知,
f′(1)=2a+(b-
| 1 |
| 2 |
| 1 |
| 2 |
解得a=1,b=-
| 1 |
| 2 |
∴f(x)=x2-x.
(2)g(x)=lnx-f(x)f′(x)=lnx-2x3+3x2-x;
∵g′(x)=
| (x-1)(6x2+1) |
| x |
∴当x∈(0,1)时,g(x)单调递增;当x∈(1,+∞)时,g(x)单调递减.
∴当x=1时,g(x)有最大值,且gmax(x)=0;
(3)x>0时,不等式x2+
| 1 |
| x2 |
| 1 |
| x |
| 1 |
| x |
令x+
| 1 |
| x |
| 4 |
| t |
∴lnm≤(t-
| 4 |
| t |
∴0<m≤
| 1 |
| e |
点评:本题考查了导数的综合应用及恒成立问题,同时考查了换元法的应用,属于中档题.

练习册系列答案
相关题目
已知变量x、y满足约束条件
,则目标函数z=3x-y的最大值是( )
|
| A、6 | ||
| B、-1 | ||
| C、1 | ||
D、
|
关于三条不同直线a,b,l以及两个不同平面α,β,下面命题正确的是( )
| A、若a∥α,b∥α,则a∥b |
| B、若a∥α,b⊥α,则b⊥α |
| C、若a⊥α,α∥β,则α⊥β |
| D、若a?α,b?α,且l⊥a,l⊥b,则l⊥α |
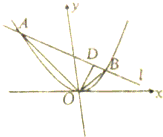 如图,已知直线l与顶点在原点O,焦点在y轴的正半轴上的抛物线C相交于A,B两点,且OA⊥OB,垂足D的坐标为(1,2).
如图,已知直线l与顶点在原点O,焦点在y轴的正半轴上的抛物线C相交于A,B两点,且OA⊥OB,垂足D的坐标为(1,2).