题目内容
已知定义在(0,
)上的函数f(x)的导函数为f′(x),且对任意x∈(0,
),都有f′(x)sinx<f(x)cosx,则不等式f(x)<2f(
)sinx的解集为 .
| π |
| 2 |
| π |
| 2 |
| π |
| 6 |
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:根据条件,构造函数g(x)=
,求函数的导数,利用导数即可求出不等式的解集.
| f(x) |
| sinx |
解答:
解:由f′(x)sinx<f(x)cosx,
则f′(x)sinx-f(x)cosx<0,
构造函数g(x)=
,
则g′(x)=
,
当x∈(0,
)时,g′(x)=
<0,
即函数g(x)在(0,
)上单调递减,
则不等式式f(x)<2f(
)sinx等价为式
<
=
,
即g(x)<g(
),
则
<x<
,
故不等式的解集为(
,
),
故答案为:(
,
)
则f′(x)sinx-f(x)cosx<0,
构造函数g(x)=
| f(x) |
| sinx |
则g′(x)=
| f′(x)sinx-f(x)cosx |
| sin2x |
当x∈(0,
| π |
| 2 |
| f′(x)sinx-f(x)cosx |
| sin2x |
即函数g(x)在(0,
| π |
| 2 |
则不等式式f(x)<2f(
| π |
| 6 |
| f(x) |
| sinx |
f(
| ||
|
f(
| ||
sin
|
即g(x)<g(
| π |
| 6 |
则
| π |
| 6 |
| π |
| 2 |
故不等式的解集为(
| π |
| 6 |
| π |
| 2 |
故答案为:(
| π |
| 6 |
| π |
| 2 |
点评:本题主要考查不等式的 求解,根据条件构造函数,利用函数的单调性和导数之间的关系是解决本题的关键.

练习册系列答案
相关题目
 图是某赛季甲、乙两名篮球运动员每场比赛得分统计的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是( )
图是某赛季甲、乙两名篮球运动员每场比赛得分统计的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是( )| A、62 | B、63 | C、64 | D、65 |
曲线y=x3-2x2-4x+2在点(1,-3)处的切线方程是( )
| A、5x+y+2=0 |
| B、5x+y-2=0 |
| C、5x-y-8=0 |
| D、5x-y+8=0 |
如果如图程序执行后输出的结果是143,那么在程序until后面的“条件”应为( )

| A、i>9 | B、i>=9 |
| C、i<=9 | D、i<9 |
设(-∞,a)为f(x)=
反函数的一个单调递增区间,则实数a的取值范围为 ( )
| 1-2x |
| x-2 |
| A、a≤2 | B、a≥2 |
| C、a≤-2 | D、a≥-2 |
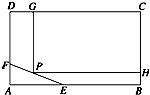 如图,长方形ABCD形状的空地,AB=100m,BC=80m,现决定在该空地上规划出一块矩形CGPH地面学生公寓,要求一边落在CD 上,但不得越过文物保护区△AEF的EF.△AEF的边AE=30m,AF=20m.
如图,长方形ABCD形状的空地,AB=100m,BC=80m,现决定在该空地上规划出一块矩形CGPH地面学生公寓,要求一边落在CD 上,但不得越过文物保护区△AEF的EF.△AEF的边AE=30m,AF=20m.