题目内容
1．已知a＞0，x，y满足约束条件$\left\{\begin{array}{l}x≥1\\ x+y≤2\\ ax-y-2a≤0\end{array}\right.$，z=x+2y的最小值为-2，则a=（ ）| A． | $\frac{1}{2}$ | B． | $\frac{3}{2}$ | C． | 1 | D． | 2 |
分析 由约束条件作出可行域，数形结合得到最优解，联立方程组求得最优解的坐标，代入ax-y-2a=0得答案．
解答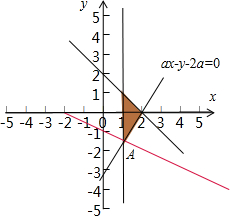 
解：由约束条件$\left\{\begin{array}{l}x≥1\\ x+y≤2\\ ax-y-2a≤0\end{array}\right.$，作出可行域如图，
联立$\left\{\begin{array}{l}{x=1}\\{x+2y=-2}\end{array}\right.$，解得A（1，-$\frac{3}{2}$），z=x+2y的最小值为-2，
由图形可知A是目标函数的最优解，A在ax-y-2a=0上，
可得：a+$\frac{3}{2}$-2a=0
解得a=$\frac{3}{2}$．
故选：B．
点评 本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题．
练习册系列答案
名校课堂系列答案
相关题目
12．
2016年某省人社厅推出15项改革措施，包括机关事业单位基本养老保险制度改革、调整机关事业单位工资标准、全省县以下机关建立职务与职级并行制度．某市为了了解该市市民对这些改革措施的态度，在该市随机抽取了50名市民进行调查，作出了他们月收入（单位：百元，范围：[15，75]）的频率分布直方图，同时得到其中各种月收入情况的市民对该项政策赞成的人数统计表．
（1）求月收入在百元内的频率，并补全这个频率分布直方图，在图中标出相应的纵坐标；
（2）根据频率分布直方图估计这50人的平均月收入；
（3）为了这个改革方案能够更好的实施，从这些调查者中选取代表提供建议，若从月收入在[35，45）百元和[65，75]百元的不赞成的被调查者中随机抽取2人，求这两名代表月收入差不超过1000元的概率．
2016年某省人社厅推出15项改革措施，包括机关事业单位基本养老保险制度改革、调整机关事业单位工资标准、全省县以下机关建立职务与职级并行制度．某市为了了解该市市民对这些改革措施的态度，在该市随机抽取了50名市民进行调查，作出了他们月收入（单位：百元，范围：[15，75]）的频率分布直方图，同时得到其中各种月收入情况的市民对该项政策赞成的人数统计表．| 月收入 | 赞成人数 |
| [15，25） | 4 |
| [25，35） | 8 |
| [35，45） | 12 |
| [45，55） | 5 |
| [55，65） | 2 |
| [65，75] | 2 |
（2）根据频率分布直方图估计这50人的平均月收入；
（3）为了这个改革方案能够更好的实施，从这些调查者中选取代表提供建议，若从月收入在[35，45）百元和[65，75]百元的不赞成的被调查者中随机抽取2人，求这两名代表月收入差不超过1000元的概率．
9．函数$f（x）=Asin（ωx+\frac{π}{4}）（ω＞0）$的图象与x轴交点的横坐标构成一个公差为$\frac{π}{3}$的等差数列，要得到函数g（x）=Acosωx的图象，只需将f（x）的图象（ ）
| A． | 向左平移$\frac{π}{12}$个单位 | B． | 向右平移$\frac{π}{4}$个单位 | ||
| C． | 向左平移$\frac{π}{4}$个单位 | D． | 向右平移$\frac{3π}{4}$个单位 |
6．已知集合A={x|x2-3x-10＜0，x∈N*}，B={2x＜16}，则A∩B=（ ）
| A． | {-1，0，1，2，3} | B． | {1，2，3，4} | C． | {1，2，3} | D． | {1} |
10．已知α为第二象限角，sin（π+α）=-$\frac{1}{3}$，则tanα=（ ）
| A． | -$\frac{\sqrt{2}}{4}$ | B． | $\frac{\sqrt{2}}{4}$ | C． | -$\frac{\sqrt{2}}{2}$ | D． | $\frac{\sqrt{2}}{2}$ |