题目内容
16.已知函数f(x)=alnx-x-$\frac{a}{x}$+2a(其中a为常数,a∈R).(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)当a>0时,是否存在实数a,使得当x∈[1,e]时,不等式f(x)>0恒成立?如果存在,求a的取值范围;如果不存在,说明理由(其中e是自然对数的底数,e=2.71828…)
分析 (Ⅰ)求出函数f(x)的导数,通过讨论a的范围,求出函数的单调区间即可;
(Ⅱ)通过讨论a的范围,根据函数的单调性求出f(x)的最小值,从而确定a的范围即可.
解答 解:(Ⅰ)由于f(x)=alnx-x-$\frac{a}{x}$+2a,(x>0),
f′(x)=$\frac{{-x}^{2}+ax+a}{{x}^{2}}$,
①a≤0时,f′(x)<0恒成立,
于是f(x)的递减区间是(0,+∞),
②a>0时,令f′(x)>0,解得:0<x<$\frac{a+\sqrt{{a}^{2}+4a}}{2}$,
令f′(x)<0,解得:x>$\frac{a+\sqrt{{a}^{2}+4a}}{2}$,
故f(x)在(0,$\frac{a+\sqrt{{a}^{2}+4a}}{2}$)递增,在($\frac{a+\sqrt{{a}^{2}+4a}}{2}$,+∞)递减;
(Ⅱ)a>0时,
①若$\frac{a+\sqrt{{a}^{2}+4a}}{2}$≤1,即0<a≤$\frac{1}{2}$,此时f(x)在[1,e]递减,
f(x)min=f(e)=3a-e-$\frac{a}{e}$=(3-$\frac{1}{e}$)a-e≤(3-$\frac{1}{e}$×$\frac{1}{2}$-e<0,
f(x)>0恒成立,不合题意,
②若$\frac{a+\sqrt{{a}^{2}+4a}}{2}$>1,$\frac{a+\sqrt{{a}^{2}+4a}}{2}$<e,
即$\frac{1}{2}$<a<$\frac{{e}^{2}}{e+1}$时,
此时f(x)在(1,$\frac{a+\sqrt{{a}^{2}+4a}}{2}$)递增,在($\frac{a+\sqrt{{a}^{2}+4a}}{2}$,e)递减,
要使在[1,e]恒有f(x)>0恒成立,
则必有$\left\{\begin{array}{l}{f(1)>0}\\{f(e)>0}\end{array}\right.$,则$\left\{\begin{array}{l}{a-1>0}\\{3a-e-\frac{a}{e}>0}\end{array}\right.$,
解得:$\frac{{e}^{2}}{3e-1}$<a<$\frac{{e}^{2}}{e+1}$;
③若$\frac{a+\sqrt{{a}^{2}+4a}}{2}$≥e,即a≥$\frac{{e}^{2}}{e+1}$时,
f(x)在[1,e]递增,令f(x)min=f(1)=a-1>0,
解得:a≥$\frac{{e}^{2}}{e+1}$,
综上,存在实数a∈($\frac{{e}^{2}}{3e-1}$,+∞),使得f(x)>0恒成立.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道综合题.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案| A. | {x|1≤x<3} | B. | {x|x<3} | C. | {x|x≤-1} | D. | {x|-1<x<1} |
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 1 | D. | 2 |
| A. | -$\frac{1}{9}$ | B. | -9 | C. | $\frac{1}{9}$ | D. | 9 |
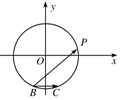 已知△ABC中,BC=1,AB=$\sqrt{3}$,AC=$\sqrt{6}$,点P是△ABC的外接圆上的一个动点,则$\overrightarrow{BP}$•$\overrightarrow{BC}$的最大值是( )
已知△ABC中,BC=1,AB=$\sqrt{3}$,AC=$\sqrt{6}$,点P是△ABC的外接圆上的一个动点,则$\overrightarrow{BP}$•$\overrightarrow{BC}$的最大值是( )| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}+1$ |
| A. | i | B. | -i | C. | -1 | D. | 1 |